bestimmen Sie eine ganzrationale Funktion 4 Grades deren Graph Achsen symmetrisch zur X Achse ist, in B(2/0) die …

Question

Aufgabe:

bestimmen Sie eine ganzrationale Funktion 4 Grades deren Graph Achsen symmetrisch zur X Achse ist, in B(2/0) die Steigung m=2  hat und einen Wendepunkt bei x=-1 besitzt

Problem/Ansatz:

Dies habe ich bisher getan:
f(x)=ax⁴+bx²+c
f‘(x)=4ax³+2bx
f‘‘(x)= 12ax²+2b

B(2|0) —> f(2)=0–> 16a+4b+c=0
Steigung m=2 —> f‘(2)=2 —> 32a+4b=2
Wendepunkt bei x=-1 —> f‘‘(-1)=0 —> 12a+2b=0

Also habe ich jetzt das lineare Gleichungssystem:
16a+4b+c=0
32a+4b=2
12a+2b=0

Irgendwie komme ich nicht weiter, weil x noch unbekannt ist. Kann mir wer weiterhelfen?

Answer 1

Hallo,

das sieht doch schon gut aus.

16a+4b+c=0  (1)

32a+4b=2      (2)

12a+2b=0      (3)

Mit (2) und (3) kannst du jetzt a und b bestimmen und am Schluss c mit (1).

0,5*(2) - (3)

4a = 1

a=0,25

in (3) → 3+2b=0 → b=-1,5

in (1) → 4-6+c=0 → c=2

f(x)=0.25x⁴-1.5x²+2

Comments

Gemeint ist wohl Symmetrie zur y-Achse.

Answer 2

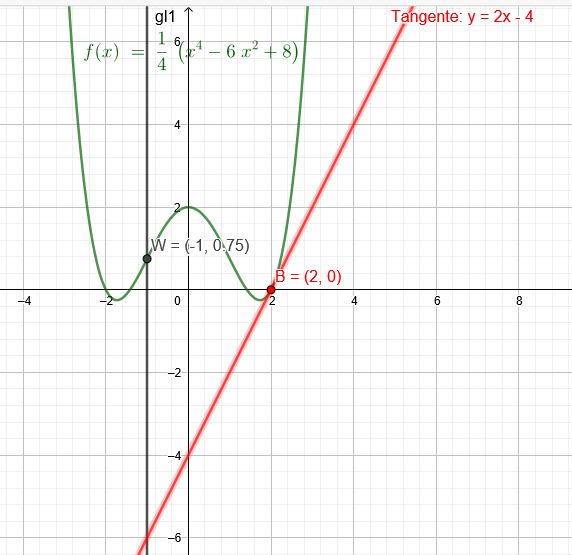
Bestimmen Sie eine ganzrationale Funktion 4. Grades deren Graph achsensymmetrisch zur y- Achse ist, in $B(2|0)$ die Steigung $m=2$  hat und einen Wendepunkt bei $x=-1$ besitzt

$B(2|0)$ →  $A(-2|0)$

$f(x)=a(x-2)(x+2)(x-N)(x+N)$

$f(x)=a[(x^2-4)(x^2-N^2)]=a[x^4-N^2x^2-4x^2+4N^2]$

$f'(x)=a[4x^3-2N^2x-8x]$

$f''(x)=a[12x^2-2N^2-8]$

Wendepunkt bei $x=-1$

$f''(-1)=a[12-2N^2-8]=0$

$N^2=2$

$f'(x)=a[4x^3-12x]$

in $B(2|...)$ die Steigung $m=2$

$f'(2)=a[4\cdot 2^3-12\cdot2] =8a=2$

$a=\frac{1}{4}$

$f(x)=\frac{1}{4}[x^4-2x^2-4x^2+4\cdot 2]$

$f(x)=\frac{1}{4}(x^4-6x^2+8)$