Unendliche Reihen berechnen

Question

Unendliche Reihen

Leider habe ich Probleme beim Lösen folgender Aufgabe! Kann mir jemand beim Ansatz weiterhelfen?

Aufgabe:

Berechnen Sie folgende Reihe. Betrachten Sie dazu die Folge der Partialsummen.

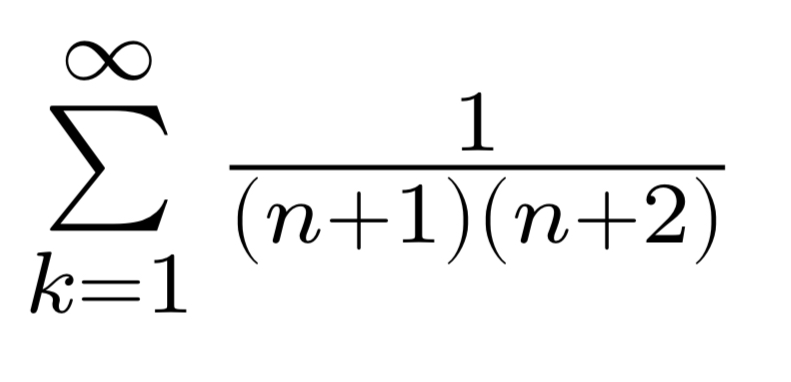
Text erkannt:

$\sum \limits_{k=1}^{\infty} \frac{1}{(n+1)(n+2)}$

Comments

Partialbruchzerlegung:

A/(n+1) + B/(n+2) = 1/((n+1)(n+2))

Answer 1

Aloha :)

Willkommen in der Mathelounge... \o/

Setze zunächst eine obere Grenze $N$ und teile die Summe in zwei Summen auf:$$S_N\coloneqq\sum\limits_{n=1}^N\frac{1}{(n+1)(n+2)}=\sum\limits_{n=1}^N\left(\frac{1}{n+1}-\frac{1}{n+2}\right)=\sum\limits_{n=1}^N\frac{1}{n+1}-\sum\limits_{n=1}^N\frac{1}{n+2}$$$$\phantom{S_N}=\sum\limits_{n=1}^N\frac{1}{n+1}-\sum\limits_{n=2}^{N+1}\frac{1}{n+1}=\left(\frac{1}{1+1}+\sum\limits_{n=2}^N\frac{1}{n+1}\right)-\left(\sum\limits_{n=2}^{N}\frac{1}{n+1}+\frac{1}{N+2}\right)$$$$\phantom{S_N}=\frac12-\frac{1}{N+2}$$Nun ist der Grenzwert klar:$$\lim\limits_{N\to\infty}S_N=\lim\limits_{N\to\infty}\left(\frac12-\frac{1}{N+2}\right)=\frac12$$

Comments

Vielen, vielen Dank! :-)