Untersuchen Sie die Funktion auf Stetigkeit

Question

Aufgabe:

Die Aufgabe lautet: Untersuchen Sie die Funktion auf Stetigkeit.

f(x)=1/x-1

Problem/Ansatz:

Ich weiß, dass ich die Grenzwerte der Funktion bestimmen muss, um zu sehen, ob sie stetig ist. Wie man Grenzwerte ausrechnet weiß ich prinzipiell, jedoch weiß ich nicht , gegen was x streben muss und auch nicht, wie ich das herausfinden könnte. Außerdem verwirrt mich immer linke und rechte Seite.

Vielen Dank im Voraus :)

Comments

Geht es um

$$f(x)= \frac{1}{x}-1 \text{ ODER } f(x)=\frac{1}{x-1}$$

(Korrekt gestellt wäre die Aufgabe eigentlich auch nur mit der Angabe eines Definitionsbereichs).

Answer 1

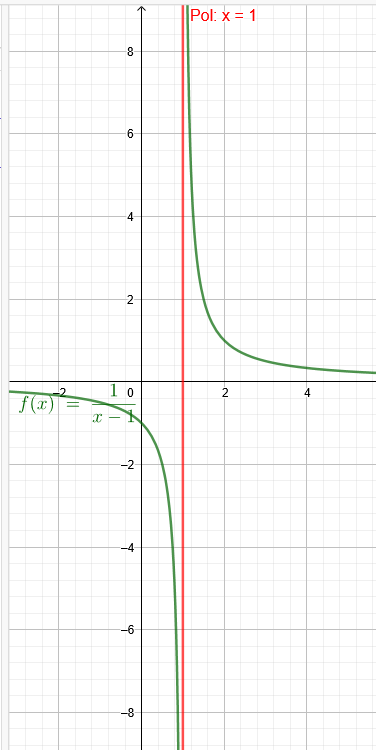
Die Aufgabe lautet: Untersuchen Sie die Funktion auf Stetigkeit.

f(x)=$\frac{1}{x-1}$  Diese Funktion hat einen Pol bei x=1. Sie ist dort nicht definiert. Also handelt es sich um eine unstetige Funktion.

1.)Schauen wir wie der Graph nun bei x=1,1  (ist rechts von der Polstelle) ausschaut.

f(1,1)=$\frac{1}{1,1-1}$=$\frac{1}{0,1}$=10

Rücken wir nun immer näher an x=1 ran, so wird der Funktionswert immer größer. Letztendlich geht er  gegen +∞.

Nun x=0,9 (ist links von der Polstelle)

f(0,9)=$\frac{1}{0,9-1}$=-10

Dann x=0,99

f(0,99)=$\frac{1}{0,99-1}$=-100

Hier nun läuft er gegen -∞.

Comments

Danke, dass hat mir sehr weitergeholfen!

---

Interessante Annahme. Tipp für luckylooser23: Einfach mal noch genau hinschauen, ob da in der Fragestellung Klammern fehlen oder nicht.

Plotlux öffnen

f₁(x) = 1/x-1f₂(x) = 1/(x-1)x = 1

---

Ich würde doch mal gerne wissen, wie man bei 1/x-1 sicher sein kann, dass 1/(x-1) gemeint ist??

---

Wenn es sich um f(x)=$\frac{1}{x}$-1 handeln sollte, wäre doch der von mir notierte Weg auch zielführend.

---

Im Prinzip ja. "Die Aufgabe lautet: Untersuchen Sie die Funktion auf Stetigkeit. "

" Der Graph von f(x)=1/x -1. Diese Funktion hat einen Pol bei x=0. f ist dort nicht definiert. Also handelt es sich um eine unstetige Funktion."

Auch wenn definiert wäre, dass f(0):= 0 oder f(1):=0 je nach Fragestellung, ist f nicht stetig.

Answer 2

Mit der Folgenkriterium kannst du überprüfen, ob eine Funktion stetig ist oder nicht. Dabei muss gelten dass für alle Folgen x_n gilt, wo bei lim n->unendlich x_n=x

lim n->unendlich f(x_n)= f(lim n->unendlich x_n)=f(x).

Wenn du eine Folge findest, bei der das nicht gilt, kannst du dir sicher sein, dass die Funktion nicht stetig ist.

Comments

Dieser Beitrag hat nichts mit der Frage zu tun - um es mal diplomatisch zu formulieren.

---

Habe es abgeändert, ist es jetzt besser so?