Wie beweist man folgende Aussage zu einem Polynom?

Question

Gegeben ist folgende Aufgabe:

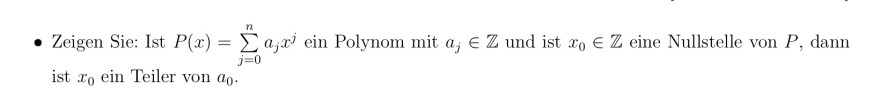
Text erkannt:

- Zeigen Sie: Ist \( P(x)=\sum \limits_{j=0}^{n} a_{j} x^{j} \) ein Polynom mit \( a_{j} \in \mathbb{Z} \) und ist \( x_{0} \in \mathbb{Z} \) eine Nullstelle von \( P \), dann ist \( x_{0} \) ein Teiler von \( a_{0} \).

Wie löse ich folgende Aufgabe? Mein Ansatz wäre die Summe anschließend als Linearfaktorzerlegung auszuschreiben, ich weiß aber nicht ob diese Idee überhaupt Sinn macht. Würde mich über Hilfe sehr freuen;)

Answer 1

Hallo

ja, wenn x0 eine Nullstelle ist kann man immer (x-x0) ausklammern, und hat dann (x-x0)*q(x) mit q(x) vom Grade (n-1), beim ausmultiplizieren  dann benutzen, dass a0 ganz ist.  und nur das absolute Glied von q mal x0 =a0 von P ist

Gruß lul

Comments

Vielen Dank für deine Antwort, jedoch verstehe ich sie nicht komplett. Wie meinst du das mit dem Ausmultiplizieren und der Annahme, dass a0 gerade ist?

---

ao ist ganz nicht gerade! wo soll ich das gesagt haben?

Schreibe q(x) allgemein hin, multipliziere so aus dass man sieht was x0* dem absoluten Glied von q ist

lul

---

Tut mir leid ich hatte zu schnell gelesen gehabt vielen Dank für die Antwort

Answer 2

\(P(x_0)=\sum_{j=0}^n a_jx_0^i=0\), also

\(a_0=-\sum_{j=1}^n a_jx_0^j=x_0\cdot(- \sum_{j=1}^na_jx_0^{j-1})\),

q.e.d.

Comments

Danke für die Antwort, leider ist für mich nicht ersichtlich, wo der Beweis des Teilens vorkommt

---

Da steht doch, dass \(a_0\) ein ganzzahliges Vielfaches von \(x_0\) ist.

---

"\(x_0\) ist ein Teiler von \(a_0\)" bedeutet definitionsgemäß,

dass es eine ganze Zahl \(z\) gibt mit \(a_0=x_0\cdot z\).