Den 1. Bruch habe ich mit \( (1-x)^{2} \) erweitert, damit gleiche Nenner da sind. Dann alles auf einen Bruchstrich und vereinfachen.
lim_(x↦1+)\( \frac{-2x+x^2-2}{(1-x)^3} \)
Hier setze ich x=1,1
\( \frac{-2*1,1+1,1^2-2}{(1-1,1)^3} \)=\( \frac{-2,2+1,1^2-2}{(-0,1)^3} \)=2990
lim_(x↦1-) Hier setze ich x=0,9
\( \frac{-2*0,9+0,9^2-2}{(1-0,9)^3} \) =-2990
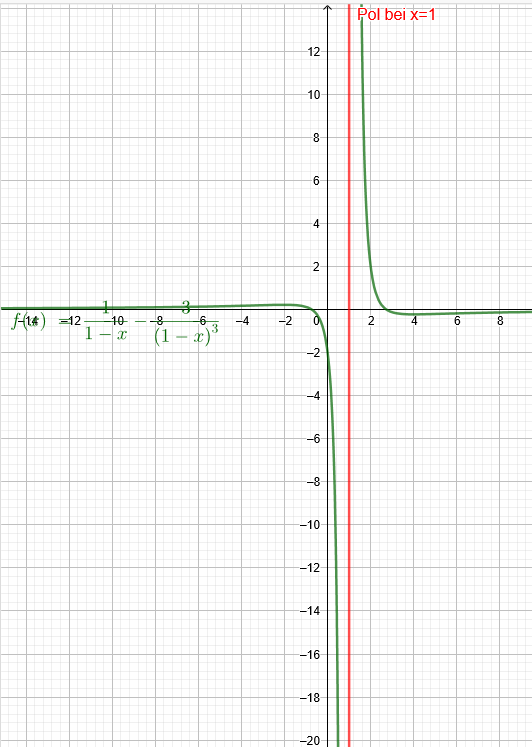
Hier der Verlauf des Graphen: