Extremstellen Berechnen (e-Funktion)

Question

Aufgabe: Berechne von der Folgenden Funktion die Extermsellen h(x)= x² * e^x

Problem/Ansatz: Habe ich ein Fehler bei der Not. Bed. gemacht?

Ableitungen: h'(x)= 2x * e^x         (und später für die Hin. Bed.   h''(x)= 2*e^x)

Not. Bed. :

2x*e^x=0 /-2x

e^x=-2x /ln

x= ln(-2)

Answer 1

Hallo

Deine Ableitung ist falsch! Produktregel u=x²  u'=2x: v=e^x v'=e^x

(uv)'=u'v+uv'  den zweiten Term hast du vergessen.

(allerdings ist auch deine Rechnung im Rest sehr falsch! 2x*ex=0 /-2x wenn man 2x abzieht verschwindet es auf der linken Seite doch nicht?)

Gruß lul

Comments

okay, danke. ist die Lösung = 2e^x + 2x + x² nachdem ich die Produktregel angewendet habe richtig ?

---

korrigiere mich : 2e^x + 2x + x²

---

Nein, immer noch sehr falsch, du hattest den ersten Term mit 2xe^x richtig, jetzt noch uv* addieren.

lul

Answer 2

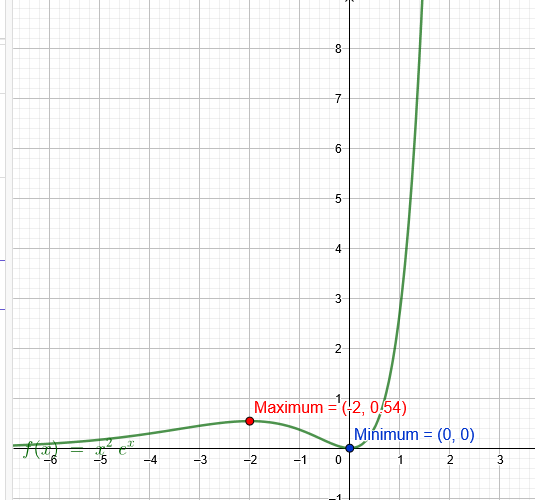
h(x)= $x^{2}$ * $e^{x}$

h´(x)= 2x * $e^{x}$+$x^{2}$ * $e^{x}$

2x * $e^{x}$+$x^{2}$ * $e^{x}$=0

$e^{x}$*($x^{2}$+2x)=0     $e^{x}$ kann nicht 0 werden

$x^{2}$+2x=0

x*(x+2)=0

x₁=0      h(0)=0

x₂=-2    h(-2)= $(-2)^{2}$ * $e^{-2}$=$\frac{4}{e^2}$

Art des Extremwertes:

h´´(x)=2 * $e^{x}$+2x* $e^{x}$+2x*$e^{x}$+$x^{2}$ * $e^{x}$=

h´´(x)=2 * $e^{x}$+4x* $e^{x}$+$x^{2}$ * $e^{x}$

1.) h´´(0)=2 * $e^{0}$=2>0 Minimum

2.)h´´(-2)=2 * $e^{-2}$+4*(-2)* $e^{-2}$+$(-2)^{2}$ * $e^{-2}$

h´´(-2)=2 * $e^{-2}$-8* $e^{-2}$+4* $e^{-2}$=-2* $e^{-2}$<0 Maximum