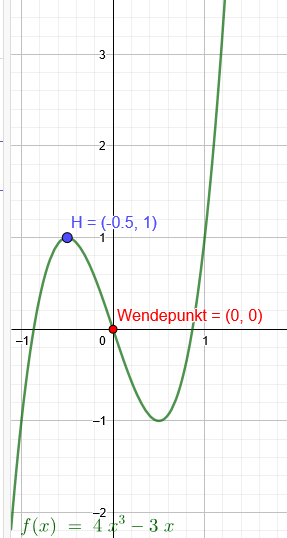
Der Graph einer ganzrationalen Funktion 3. Grades ist punktsymmetrisch zum Ursprung und hat den Hochpunkt H(-\( \frac{1}{2} \) | 1)
f(x)=a*x^3+bx
f(-\( \frac{1}{2} \))=a*(-\( \frac{1}{2} \))^3+b*(-\( \frac{1}{2} \))
1.)-\( \frac{1}{8} \)*a-\( \frac{1}{2} \)*b=1
f´(x)=3ax^2+b
f´(-\( \frac{1}{2} \))=3a*(-\( \frac{1}{2} \))^2+b
2.)\( \frac{3}{4} \)a+b=0 → b=-\( \frac{3}{4} \)a in1.)
-\( \frac{1}{8} \)*a-\( \frac{1}{2} \)*(-\( \frac{3}{4} \)a)=1
-\( \frac{1}{8} \)*a+\( \frac{3}{8} \)a=1
a=4 b=-3
f(x)=4*x^3-3x