Eulerscher Multiplikator zur Differentialgleichung

Question

Aufgabe:

Gelöst werden soll die Differentialgleichung y - xy² + (x + x²y²) * y' = 0 mit y(1) = 1.

Ich weiß bereits, dass die DGL nicht exakt ist. Allerdings finde ich keinen eulerschen Multiplikator, sodass die DGL gelöst werden kann.

Über Hilfe wäre ich sehr dankbar.

Answer 1

Hallo,

Py=1-2xy

Qx=1+2y² *x ----->nicht exakt

Die oft verwendeten Formeln des integr, Faktors nach x oder y führen hier nicht zum Erfolg

Da in der DGL das Produkt z=x*y vorkommt, gibt es dazu eine spez.Formel:

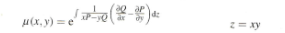
Ich habe erhalten μ = $\frac{1}{x^2 y^2}$