Berechnen Sie die Koordinaten des Neupunktes C mithilfe der bekannten Punkte A und B!

Question

Aufgabe:

Text erkannt:

Berechnen Sie die Koordinaten des Neupunktes C mithilfe der bekannten Punkte A und B!
$a=134,6964$ gon
$s_{B, C}=19,422 \mathrm{~m}$
\begin{tabular}{|c|c|c|}
\cline { 2 - 3 } \multicolumn{1}{c|}{} & $\mathrm{y}$ & $\mathrm{x}$ \\
\hline $\mathrm{A}$ & 14,913 & 11,720 \\
\hline $\mathrm{B}$ & 42,721 & 28,223 \\
\hline
\end{tabular}

Problem/Ansatz:

Ich habe Leider keinen Ansatz, wäre sehr dankbar wenn mir da jemand weiter helfen kann.

Answer 1

Hallo,

um die Koordinaten des Neupunktes $C$ zu berechnen benötigt man noch den Richtungswinkel $\varphi$ der Strecke $BC$. Dazu folgende Skizze:

(Bem.: die X-Achse zeigt nach oben; Y nach rechts)

Der hellblaue Winkel ist der Richtungswinkel $\beta$ der Strecke $AB$. Der Richtungswinkel $\varphi$ (blau) ist die Summe aus $\beta$ und dem roten Winkel $\gamma$. Es gilt:$${\color{red}\gamma} = 200\,\text{gon} - \alpha= 65,3036\,\text{gon}\\ {\beta} = \arctan\left(\frac{B_y-A_y}{B_x-A_x} \right) =65,9027\,\text{gon} \\ \implies {\color{blue}\varphi} = \beta + {\color{red}\gamma} = 131,2063\,\text{gon}$$Ausgehend vom Punkt $B$ sind die Koordinaten von $C$:$$C_x = B_x + s_{B,C}\cdot \cos({\color{blue}\varphi}) = 19,079\,\text m \\ C_y = B_y + s_{B,C}\cdot \sin({\color{blue}\varphi}) = 59,856\,\text m$$Gruß Werner

Answer 2

Richtungsvektor AB = B-A = (27.808, 16.503)

Richtungsvektor AB um den Winkel w = -180 + (134.6964 gon) = -58.77 Grad drehen:

BC' = AB * $\begin{pmatrix} cos(w) & -sin(w) \\ sin(w) & cos(w) \end{pmatrix}$ = (28.529, -15.222)

BC' auf Länge 19.422 normieren BC'' = (17.1355, -9.1427)

C = B + BC'' = (59.8565, 19.0803)

Comments

Der Winkel ist in gon gegeben. In der Antwort wird unterstellt, es sei Grad. Daher ist das Ergebnis falsch.

---

Danke, ich habe es korrigiert.

Answer 3

|$\vec{AB}$|=|$\vec{OB}$-$\vec{OA}$|

|$\vec{AC}$| lässt sich mit den Kosinussatz bestimmen.

Der Kreis um B mit dem Radius s_BC= |$\vec{BC}$|

schneidet den Kreis um A mit dem Radius |$\vec{AC}$| in C.

Answer 4

Die Frage ist irreführend formuliert. Man kann auch noch s_B,C verwenden.

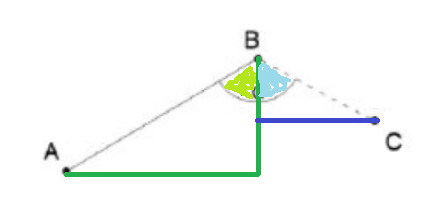
Der grün eingezeichnete Winkel ist gleich arctan((28,223 - 11,72) / (42,721 - 14,913)).

Der blau eingezeichnete Winkel ist gleich 134,6964 gon - grüner Winkel.

Für C gilt:

     (y_C - 42,721) / 19,422 = cos(blauer Winkel)

     (x_C - 28,223) / 19,422 = sin(blauer Winkel)

     Löse dieses Gleichungssystem.