f(x) = lnx
f ' (x) =1/x
f ' (e) = 1/e
Tangente. t: y = 1/e x + q
P(e|1) einsetzen. 1 = 1/e * e + q = 1 + q ==> q = 1
Tangente. t: y = 1/e x
Skizze:
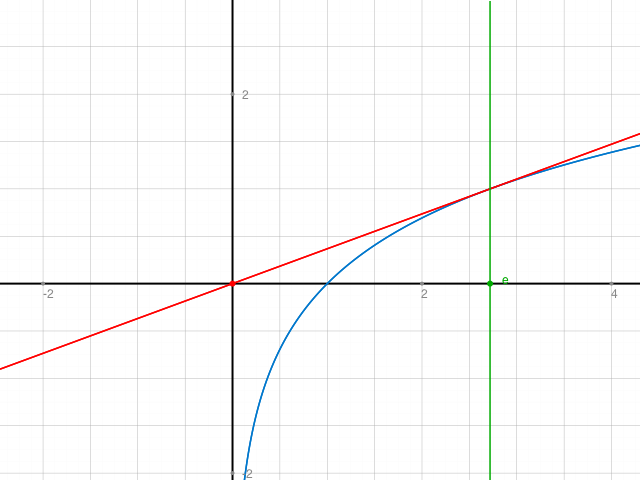
Das Dreieck O(0|0), Q(e|0), P(e|1) hat die Fläche e*1/2 = e/2
Von diesem Dreieck muss jetzt noch die Fläche unter dem blauen Bogen zwischen 1 und e subtrahiert werden.
Also ∫ ln x dx von 1 bis e.
∫ ln x dx = x*lnx - x + C
∫ ln x dx = x*lnx - x |1e = e*ln e - e - (1*ln1 - 1) = e*1 - e - (e*ln 0 - 1) = 1
Gesuchte Fläche A = e/2 - 1 ≈ 0.35914