Aufgabe:
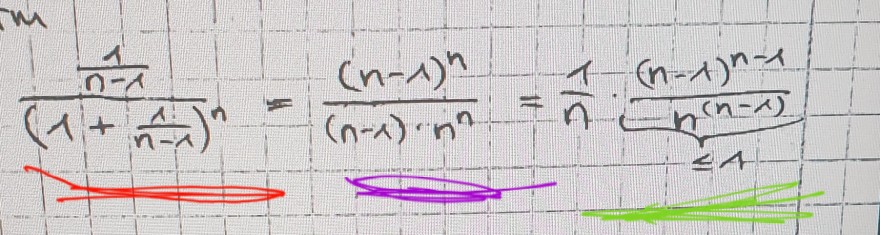
Text erkannt:
\( \frac{\frac{1}{n-1}}{\left(1+\frac{1}{n-1}\right)^{n}}=\frac{(n-1)^{n}}{(n-1) \cdot n^{n}}=\frac{1}{n} \cdot \frac{\frac{(n-1)^{n-1}}{n(n-1)}}{n \leq 1} \)
Können Sie mir bitte erklären, wie man von rot zu lila und von lila zu grün kommt? Ich verstehe das nicht ganz genau :/