Bestimme quadratische Funktion aus Scheitelpunkt S und Punkt P

Question

Aufgabe:

Bestimme eine quadratische funktion f(x)= ax² + bx + c, deren Graph den Scheitelpunkt S(3/5) hat und durch den Punkt P (4/-6) verläuft

Problem/Ansatz:

Answer 1

Hallo,

allgemeine Scheitelpunktform einer quadratischen Funktion:

\(f(x)=a(x-d)^2+e\)

Scheitelpunkt S (d|e)

Setze für x und f(x) die Koordinaten von P und für d und e die des Scheitelpunktes ein und löse nach a auf.

Gruß, Silvia

Answer 2

Löse das Gleichungssystem

a*3² + b*3 + c = 5

2a*3 + b = 0

a*4² + b*4 + c = -6

Comments

Dann kommt etwas in der Art heraus:

Answer 3

Moinsen

Zwei Möglichkeiten: Entweder du setzt für c die y Koordinate des Scheitelpunktes ein. Und stellst zwei Gleichungen auf mit den beiden Punkten, die du jeweils umstellt und auflöst um a in b zu bestimmen.

Oder du setzt den Scheitelpunkt in die Scheitelpunktform ein, löst die Klammer auf, dann benötigst du nur noch a und dafür setzt du den anderen Punkt ein und stellst nach a um

Ich empfehle Variante 2

Answer 4

Öffnungsfaktor bestimmen

a = (Py - Sy) / (Px - Sx)²
a = (-6 - 5) / (4 - 3)² = - 11

Scheitelpunktform aufstellen

f(x) = a·(x - Sx)² + Sy
f(x) = - 11·(x - 3)² + 5

Jetzt noch ausmultiplizieren

f(x) = - 11·(x - 3)² + 5
f(x) = - 11·(x² - 6·x + 9) + 5
f(x) = - 11·x² + 66·x - 99 + 5
f(x) = - 11·x² + 66·x - 94

Answer 5

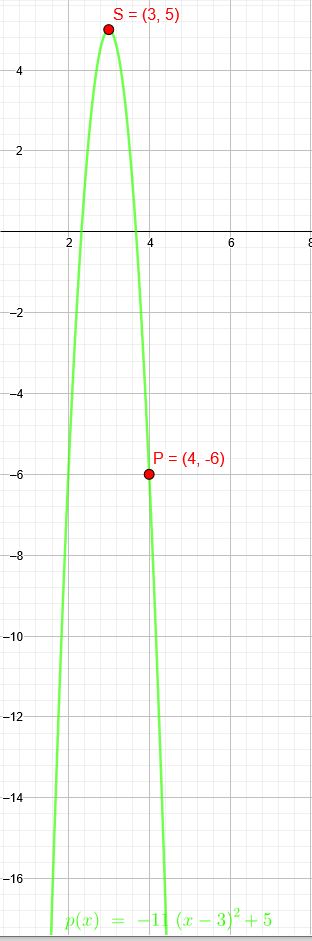
Bestimme eine quadratische Funktion \(f(x)= ax^2 + bx + c\), deren Graph den Scheitelpunkt \(S(3|\red{5})\) hat und durch den Punkt \(P (4|-6)\) verläuft.

Durch den Scheitelpunkt einer quadratischen Funktion geht eine waagerechte Tangente.

Ich verschiebe den Graphen um 5  Einheiten nach unten:

\(S´(3|\red{0})\) Dort ist nun eine doppelte Nullstelle:  \(f(x)=a*(x-3)^2\)

  \(P (4|-6)\)→\(P´ (4|-11)\)

\(f(4)=a*(4-3)^2=a=-11\)

\(f(x)=-11 \cdot (x-3)^2\)

Nun 5  Einheiten nach oben

\(p(x)=-11 \cdot (x-3)^2+5\)  Kann nun noch ausmultipliziert und zusammengefasst werden.

Comments

Das mit der doppelten Nullstelle ist eine schöne Idee.

Ich bin trotzdem entsetzt, denn du verrätst schnöde dein Lebenswerk.

Wo bleibt die quadratische Ergänzung????