Gleichung für eine Parabel aufstellen aus gegebenem Scheitelpunkt S(2|4) und Punkt C(6|0)?

Question

 

Ich bräuchte mal Hilfe. Und zwar geht es um folgende Aufgabe: 

 

Eine Parabel hat den Scheitelpunkt S(2;4) und verläuft durch den Punkt C(6;0).

Bestimme den Funktionsterm p(x) der Parabel. 

 

Ich scheiter leider schon beim Aufstellen von den Bedingungen. also die ersten zwei Bedingen sind ja nicht so schwer aber auf die dritte komm ich leider nicht... 

Die Lösung ist: -1/4x²+x+3 

 

Wäre sehr schön wenn mir jemand den Lösungsweg erklären könnte... 

für die Antworten ;) 

vlg
smilegirl

 

 

Answer 1

Eine Gleichung für eine Parabel kannst du in folgenden Formen schreiben:
f(x) = ax² + bx + c = y (Allgemeinform)
f(x) = a*(x – v)² + n = y (Scheitelpunktform)
f(x) = a*(x – x₁)*(x – x₂) = y (in Linearfaktoren)

Siehe Videos der Lektion Quadratische Funktionen!

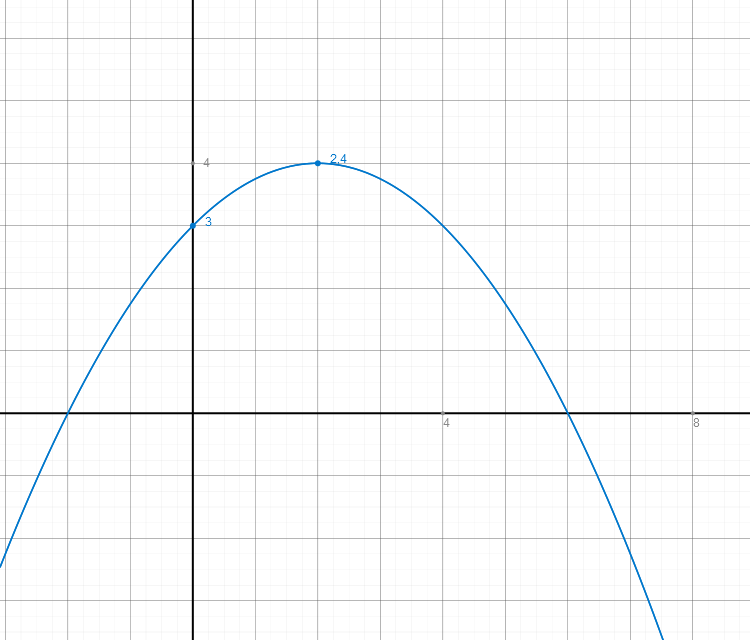
Die Koordinaten des Scheitelpunktes S(2|4) können wir der Scheitelpunktform zuordnen:
f(x) = a*(x – v)² + n
f(x) = a*(x – 2)² + 4

Jetzt können wir in diese Gleichung den Punkt C(6|0) einsetzen:
f(x) = a*(x – 2)² + 4 = y
f(6) = a*(6 – 2)² + 4 = 0

Und die Gleichung ausrechnen, um a zu ermitteln:
a*(6 – 2)² + 4 = 0
a*4² + 4 = 0
a*16 + 4 = 0   |-4
a*16 = -4    |:16
a = -4/16
a = -1/4


So wissen wir, dass a = -1/4 sein muss (der Formfaktor der Parabel, also ist sie nach unten gestreckt).

a noch einsetzen in die Funktionsgleichung:
f(x) = a*(x – 2)² + 4
f(x) = -1/4*(x – 2)² + 4

Fertig :)


Natürlich kannst du die ermittelte Funktionsgleichung noch ausmultiplizieren zur Allgemeinform:
f(x) = -1/4*(x – 2)² + 4
f(x) = -1/4*(x² – 2*2x + 4) + 4
f(x) = -1/4*x² + 1/4*4x -1/4*4 + 4
f(x) = -1/4*x² + 1x -1 + 4
f(x) = -1/4*x² + x + 3
 

Der Funktionsgraph sieht wie folgt aus:

 

Video zur Scheitelpunktform:

Teil 2 von 7 aus der Lektion Quadratische Funktionen