Bleiben wir doch mal bei deiner im Rahmen deines Ansatzes aufgestellten Gleichung
ln(x) = ax
Mit den Lösungen dieser Gleichung werden die Schnittstellen des Grafen der Funktion f(x)=ln x mit verschiedenen Ursprungsgeraden ausgedrückt.
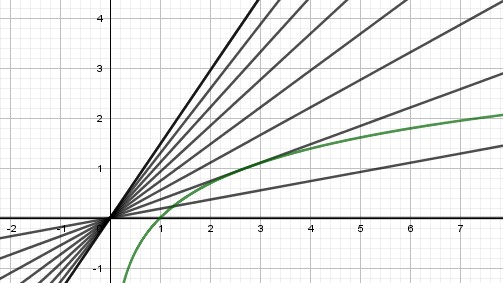
Bei a=1/e hat man eine Tangente und damit genau eine Lösung.
Für a>1/e gibt es keinen Schnittpunkt.
0< a<1/e (wird in der Skizze nur von einer Geraden repräsentiert) gibt zwei Schnittpunkte.
a=0 und auch negative a (letztere nicht abgebildet) ergeben nur einen Schnittpunkt.