Bestimme mit Hilfe des Fortsetzungssatzes jene Matrix A ∈ R4×4, welche die Projektion p2 be- schreibt.

Question

Im Vektorraum R^4x1 seien komplementäre Unterräume U₁= [{a₁, b₁}] und U₂= [{a₂, b₂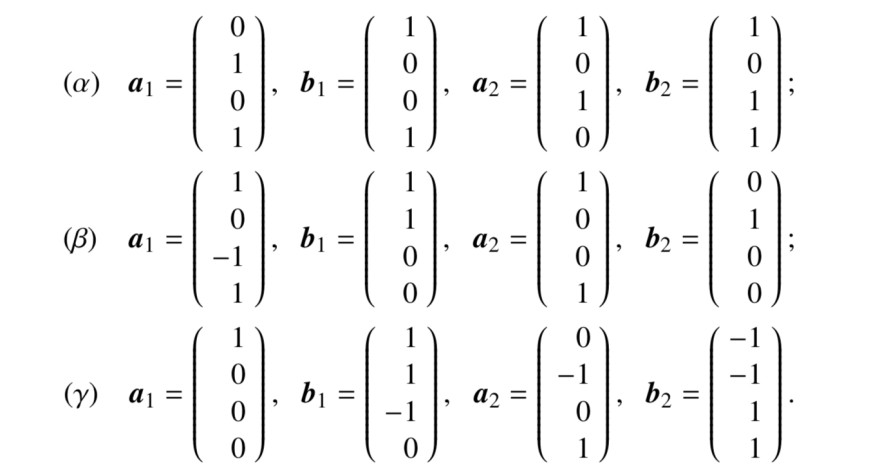

Text erkannt:

$(\alpha) \quad \boldsymbol{a}_{1}=\left(\begin{array}{c}0 \\ 1 \\ 0 \\ 1\end{array}\right), \quad \boldsymbol{b}_{1}=\left(\begin{array}{c}1 \\ 0 \\ 0 \\ 1\end{array}\right), \quad \boldsymbol{a}_{2}=\left(\begin{array}{l}1 \\ 0 \\ 1 \\ 0\end{array}\right), \quad \boldsymbol{b}_{2}=\left(\begin{array}{c}1 \\ 0 \\ 1 \\ 1\end{array}\right)$;
$(\beta) \quad \boldsymbol{a}_{1}=\left(\begin{array}{r}1 \\ 0 \\ -1 \\ 1\end{array}\right), \quad \boldsymbol{b}_{1}=\left(\begin{array}{l}1 \\ 1 \\ 0 \\ 0\end{array}\right), \quad \boldsymbol{a}_{2}=\left(\begin{array}{l}1 \\ 0 \\ 0 \\ 1\end{array}\right), \quad \boldsymbol{b}_{2}=\left(\begin{array}{l}0 \\ 1 \\ 0 \\ 0\end{array}\right)$;
$(\gamma) \quad \boldsymbol{a}_{1}=\left(\begin{array}{l}1 \\ 0 \\ 0 \\ 0\end{array}\right), \quad \boldsymbol{b}_{1}=\left(\begin{array}{r}1 \\ 1 \\ -1 \\ 0\end{array}\right), \quad \boldsymbol{a}_{2}=\left(\begin{array}{r}0 \\ -1 \\ 0 \\ 1\end{array}\right), \quad \boldsymbol{b}_{2}=\left(\begin{array}{r}-1 \\ -1 \\ 1 \\ 1\end{array}\right)$.

}]
gegeben mit

Ferner sei p2 : R4×1 → R4×1 die Projektion auf U2 in Richtung U1.
(a) Bestimme mit Hilfe des Fortsetzungssatzes jene Matrix A ∈ R4×4, welche die Projektion p2 be- schreibt.
(b) Gib für einen beliebigen Vektor v = (v1, v2, v3, v4)T ∈ R4×1 die Zerlegung in der Form v = v1 + v2 mitv1 ∈U1 undv2 ∈U2 an.

Comments

Was sagt der Fortsetzungssatz?

---

Das Prinzip der linearen Fortsetzung besagt, dass jede lineare Abbildung genau durch die Bilder der Basisvektoren bestimmt ist. Es liefert eine alternative Möglichkeit eine lineare Abbildung zu charakterisieren.

https://de.m.wikibooks.org/wiki/Mathe_für_Nicht-Freaks:_Prinzip_der_…

Answer 1

Dann ist doch z.B. p(a1) = b1 und p(a2)= b2

Und wenn man a1, a2 durch a3, a4 zu einer Basis von ℝ⁴ ergänzt, dann kann man

z.B. auch p(a3) = b1 und p(a4)= b2 hinzunehmen und hat das p bestimmt.

Comments

Nach meinem Verständnis der Vorgaben wäre

p(a1)=0, p(b1)=0,p(a2)=a2,p(b2)=b2

---

Scheint irgendwie egal zu sein.