Durch starken Wind wird er 50m weit abgetrieben
Ich nehme an, dass gemeint ist, dass die x-Koordinate seiner Position um 50 Meter größer geworden ist ... ?
Skizze:
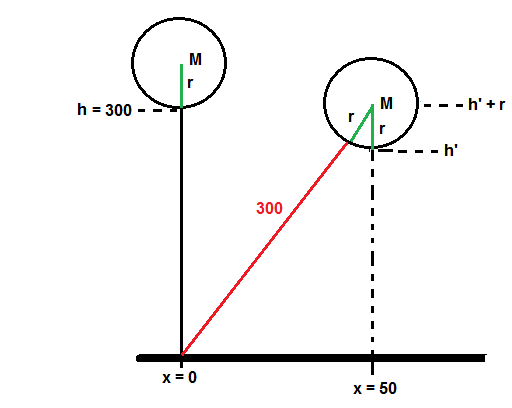
Als Höhe des Ballons definiere ich die Höhe seines tiefsten Punktes. Dies ist im ursprünglichen Zustand gleichzeitig auch der Befestigungspunkt des Halteseiles. Die Höhe dieses Punktes betrug im ursprünglichen Zustand h = 300 Meter.
Es ist zu beachten, dass im neuen Zustand der Befestigungspunkt des Halteseiles am Ballon aufgrund der Schräglage des Seiles nicht mehr der tiefste Punkt ist!
Für die neue Höhe h' gilt nach Pythagoras:
( h ' + r ) 2 + 50 2 = ( 300 + r ) 2
<=> ( h ' + r ) = √ ( ( 300 + r ) 2 - 50 2 )
<=> h ' = √ ( ( 300 + r ) 2 - 50 2 ) - r
Der tiefste Punkt des Ballons befindet sich also nun in einer
Höhe von √ ( ( 300 + r ) 2 - 50 2 ) - r Metern.
Bei einem Radius des Ballons von r = 15 Metern ergibt sich:
h ' ≈ 296 Meter