Berechnen Sie den Flächeninhalt der Fläche, die von den Graphen der Funktionen f und g begrenzt wird

Question

Aufgabe:

Berechnen Sie den Flächeninhalt der Fläche, die von den Graphen der Funktionen f mit f(x)=x-x³ und g mit g(x)=(-3/2)x² begrenzt wird.

Problem/Ansatz:

Bei dieser Aufgabe bekomme ich eine negative Wurzel wenn ich die Schnittpunkte berechne.

Kann jemand mir helfen?

Answer 1

Hallo,

es wäre natürlich einfacher, wenn du uns deinen Rechenweg zeichen würdest, um deine(n) Fehler zu erkennen.

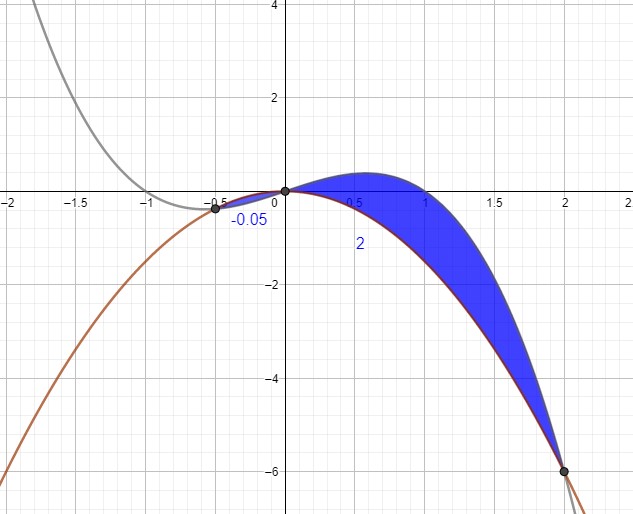
Bei mir sieht das so aus:

$x-x^{3}=-1,5 x^{2}$
$-x^{3}+1,5 x^{2}+x=0$
$x\cdot \left(-x^{2}+1,5 x+1\right)=0$
$x_1=0 \vee-x^{2}+1,5 x+1=0$
$x^{2}-1,5 x-1=0$
$x_{2,3}=0,75 \pm \sqrt{\frac{9}{16}+\frac{16}{16}}$
$x_{2,3}=0,75 \pm 1,25$

$x_2=-0,5\quad x_3=2$

Gruß, Silvia

Comments

Danke, ich habe mein Fehler gefunden. Bein nächsten Mal werde ich mein Rechenweg zeichen.☺️

---

Du Spaßvogel!    

Answer 2

Du könntest es plotten, da gibt es keine Schnittpunkte bei negativen Wurzeln oder Wurzeln von negativen Radikanden.

Answer 3

x-x³=-3/2*x²

-x³+3/2*x²+x=0

x*(-x²+3/2*x+1)=

x₁=0

-x²+3/2x+1=0

x²-3/2x-1=0

x_2,3=3/4±√(9/16+16/16)

          =3/4±√(25/16)

x₂=3/4+5/4=8/4=2

x₃=3/4-5/4=-2/4=-0,5