Zeigen, dass das Produkt f g ebenfalls n -mal differenzierbar ist mit

Question

Aufgabe:

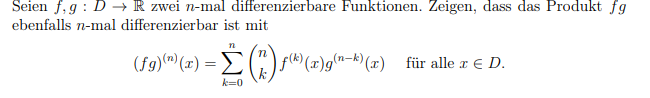
Text erkannt:

Seien $f, g: D \rightarrow \mathbb{R}$ zwei $n$-mal differenzierbare Funktionen. Zeigen, dass das Produkt $f g$ ebenfalls $n$-mal differenzierbar ist mit
$(f g)^{(n)}(x)=\sum \limits_{k=0}^{n}\left(\begin{array}{l} n \\ k \end{array}\right) f^{(k)}(x) g^{(n-k)}(x) \quad \text { für alle } x \in D .$

Answer 1

Würde ein Beweis durch Vollständige Induktion vorschlagen.