Kontrolle
4/(x-1)>2 gilt, wenn
f(x) = 4/(x-1) -2 >0
d.h. in dem Bereich, in dem der zugehörige Graph oberhalb der x-Achse verläuft.
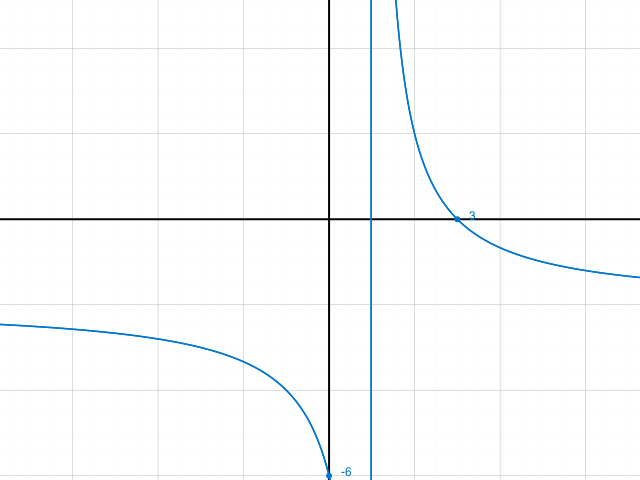
4/(x-1)>2
1 Fall: 4/(x-1)-2>0 [x > 1]
4 > 2 (x-1)
4 > 2x - 2
6 > 2x
3 > x
L={x∈ℝ | 1 < x <3}
2 Fall: 4/(x-1)-2 > 0 [x < 1]
4 < 2 (x-1)
4 < 2x - 2
6 < 2x
3 < x
L={x∈ℝ | x < 1 ∧ x > 3} = {} Leere Menge
Hier kommt doch gar nichts dazu. Es gibt keine Zahl, die kleiner als 1 und ausserdem grösser als 3 ist.
Wie fasse ich nun beide Ergebnisse zusammen?
Ich würde es so machen: L={x∈ℝ | 1 < x <3∨ (x < 1 ∧ x > 3)}
L={x∈ℝ | 1 < x <3}
Sind die ∧∨ richtig herum ?
Ja. Setze aber zur Verdeutlichung jeweils Klammern, so sieht man schneller, wenn etwas noch vereinfacht werden kann.
Die Fallunterscheidung musste aber anders beschrieben werden: x>1 und x<1 heissen die beiden Fälle.