Berechnen Sie die Länge des Rechtecks

Question

Text erkannt:

3) Gegeben sind Eckpunkte eines Rechtecks ABCD: $A=\left(\begin{array}{c}-7 \\ -3\end{array}\right), \quad B=\left(\begin{array}{l}1 \\ 3\end{array}\right)$
a) Berechnen Sie die Länge $\overline{A B}$ des Rechtecks!
b) Berechnen Sie die Koordinaten der Eckpunkte $C$ und D, wenn das Rechteck halb so breit wie lang ist!
c) Wie viel misst der Flächeninhalt des Rechtecks?
d) Wie lauten die Koordinaten des Mittelpunkts des Rechtecks?

Aufgabe:

Answer 1

a) Berechne den Betrag von $\begin{pmatrix} 1+7\\3+3 \end{pmatrix}$.

Comments

Danke.
Bitte auch die Aufgaben b,) bis d.)

---

Der Mittelpunkt von A(a|b) und B(u|v) ist M($\frac{a+u}{2}$|$\frac{b+v}{2}$).

Answer 2

Hallo,

a) Berechne die Länge des Vektors AB mit $d[A,B]:\sqrt{(b_1-a_1)^2+(b_2-a_2)^2}$

b) Die Länge der Vektoren AD und BC ist 5 und sie stehen senkrecht auf dem Vektor AB, also muss das Skalarprodukt der Vektoren gleich null sein.

$\overrightarrow{AD}=\begin{pmatrix} x+7\\y+3 \end{pmatrix}\rightarrow \quad \sqrt{(x+7)^2+(y+3)^2}=5\\ \overrightarrow{AB}\circ \overrightarrow{AD}=0\rightarrow \quad 8\cdot (x+7)+6\cdot (y+3)=0$

c) Berechne den Flächeninhalt mit Hilfe des Kreuzprodukts der Vektoren z.B. AB und AD.

d) Der Mittelpunkt des Rechtecks ist der Schnittpunkt der Diagonalen, die sich halbieren. Berechne also z.B.

$M=\overrightarrow{OA}+0,5\cdot\overrightarrow{AC}$

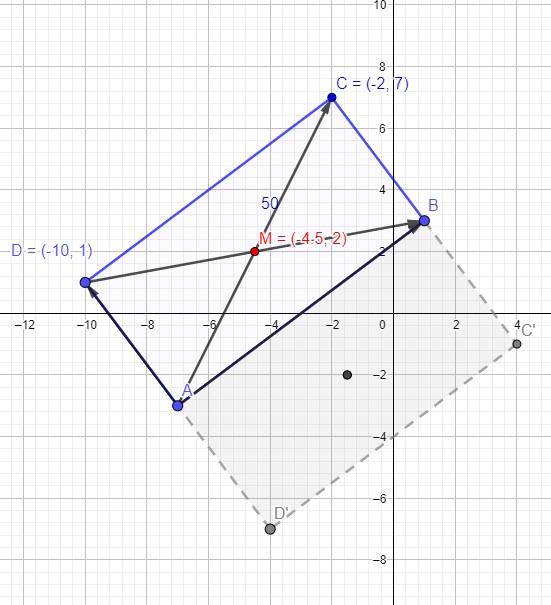
Gruß, Silvia

Comments

Vielen Dank!

---

c) Berechne den Flächeninhalt mit Hilfe des Kreuzprodukts der Vektoren z.B. AB und AD

.Das ist jetzt nicht dein Ernst?

Kreuzprodukt im R² ?

Vielleicht kann dir ggT erklären, wie man diesen Ansatz reparieren kann.

---

Ups, ich gebe zu, damit bin ich etwas über das Ziel hinausgeschossen.