Polynomfunktionen keine Lösungen

Question

Aufgabe:

\( -x^{4}+x^{2}=1+a^{2} \quad \) Losung: Subsitution \( -x^{4}+x^{2}-1 a^{2}=0 \) mit \( 0=-4 a^{2}-3<0 \)
\( \begin{array}{l} x\left(-z^{2}+z-1 a^{2}\right) \\ -z^{2}+z-1 a^{2}=0 \\ \frac{-1 \pm \sqrt{1-4 \cdot(-1) \cdot\left(-1 a^{2}\right)}}{-2} \end{array} \)

Problem/Ansatz:

Also ich verstehe nicht wie man auf die Lösung gekommen ist. Ich nehme mal an dass die meinen, die Diskriminante zu benutzen, das wäre ja alle unter der Wurzel, jedoch weiß ich nicht, was ich mit einander rechnen kann und wie ich da vorgehe. Darf ich alles direkt zusammenrechnen und muss ich die hoch 2 bei der -1a ziehen?

Answer 1

Sei \(z=x^2\), dann geht die Gleichung über in

\(-z^2+z=1+a^2\iff z^2-z+1+a^2=0=z^2+pz+q\)

mit \(p=-1\) und \(q=1+a^2\). Die Diskriminante ist

\(D=p^2-4q=1-4(1+a^2)=-3-4a^2< 0\).

Also gibt es keine reellen Lösungen.

Comments

Ich habe nicht ganz verstanden, was Sie da gemacht haben. Könnten sie das genauer erklären? Ich verstehe nämlich nicht was mit p meinen  und warum die Vorzeichen gedreht wurden.

---

Die pq-Formel kann man nur anwenden,
wenn das Polynom den höchsten Koeffizienten 1 hat,
also die Standard-Gestalt \(z^2+...\) besitzt. Deswegen nehme ich
die gegebene Gleichung mit -1 mal.

Mit \(p\) bezeichne ich den Koeffizienten von \(z\),
mit \(q\) das Absolutglied so, wie man es bei der pq-Formel
üblicherweise macht.

Answer 2

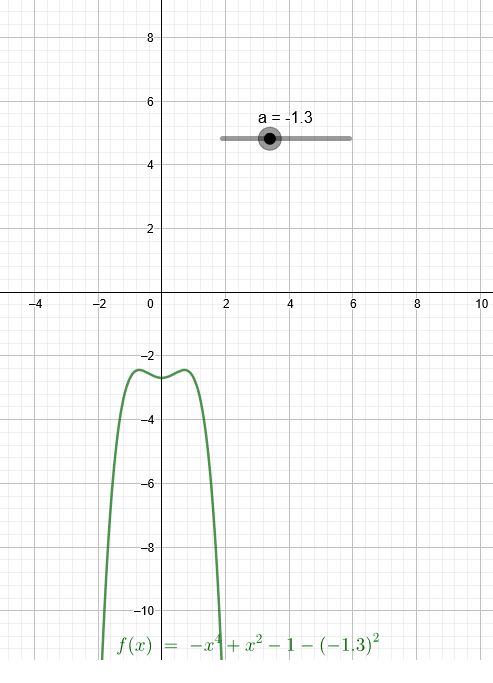
\(f_a(x)=-x^4+x^2-1-a^2\)

\(-x^4+x^2-1-a^2=0   |+1+a^2\)

\(-x^4+x^2=1+a^2    |*(-1)\)

\(x^4-x^2=-1-a^2  \)

Substitution:  \(x^2=1*z \)

\(z^2-1*z=-1-a^2  \)

\((z^2-\frac{1}{2})^2=-1-a^2 +(\frac{1}{2})^2=-1-a^2 +\frac{1}{4}=-\frac{3}{4}-a^2 =\frac{-3-4a^2}{4}      |\sqrt{~~}\)

\(z^2-\frac{1}{2}=+-\frac{1}{2}*\sqrt{-3-4a^2}\)

Egal welchen Zahlenwert du a gibst, der Term unter der Wurzel ist immer negativ. Daher gibt es keine Lösungen in  ℝ.