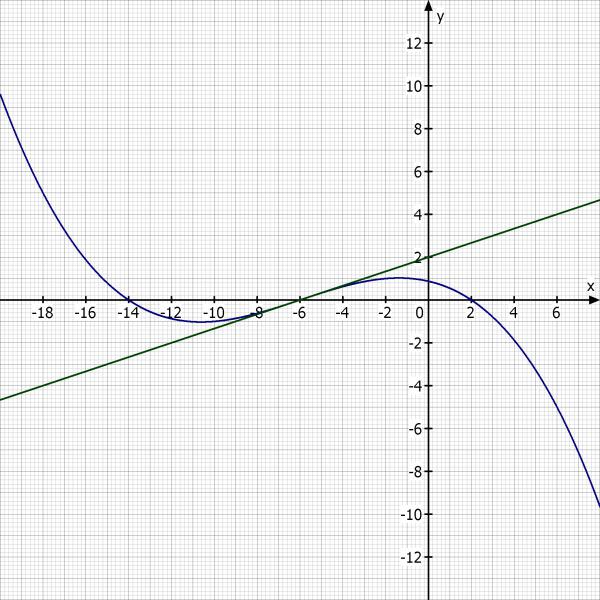
Bestimmen Sie die Gleichung einer ganzrationalen Funktion 3. Grades,
f(x) = a·x^3 + b·x^2 + c·x + d
deren Graph die x-Achse an der Stelle x = 2 schneidet,
f(2) = 0
8·a + 4·b + 2·c + d = 0
einen Wendepunkt auf der x-Achse hat und dessen Wendetangente durch die Gleichung y = 1/3 x + 2 beschrieben wird.
1/3 x + 2 = 0
x = -6
f(-6) = 0
- 216·a + 36·b - 6·c + d = 0
f'(-6) = 1/3
108·a - 12·b + c = 1/3
f''(-6) = 0
36·a - 2·b = 0
Du erhältst ein Gleichungssystem mit 4 Gleichungen und 4 Unbekannten. Probier das zunächst selber zu lösen.
Ich erhalte die Lösung a = - 1/192 ∧ b = - 3/32 ∧ c = - 11/48 ∧ d = 7/8
f(x) = - 1/192·x^3 - 3/32·x^2 - 11/48·x + 7/8
Skizze