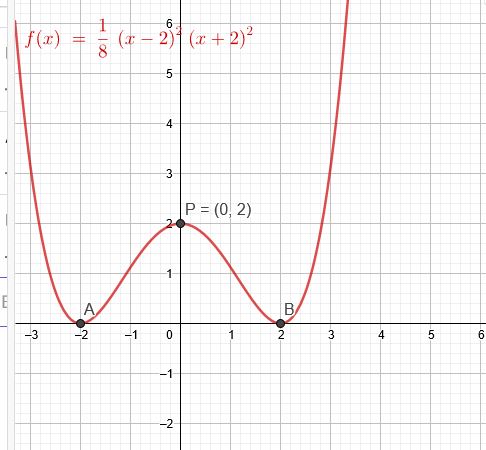
Der zur y Achse symmetrische Graph einer ganzrationalen Funktion 4. Grades geht durch P(0|2) und hat bei x=2 ein Extremum. Er berührt dort die x-Achse.
\(f(x)=a*(x-2)^2*(x+2)^2\)
\(P(0|2)\)
\(f(0)=a*(0-2)^2*(0+2)^2=16a=2\)
\(a=\frac{1}{8}\)
\(f(x)=\frac{1}{8}*(x-2)^2*(x+2)^2\)