Habe hier folgenden Beweis zum Kosinussatz:
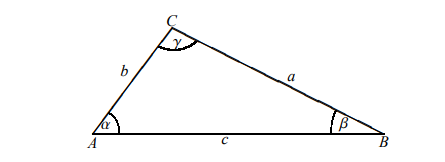
Wir betrachten zunächst den Fall \( \gamma \leq 90^{\circ}, \alpha \leq 90^{\circ} \). Wir zeichnen in ein solches Dreieck die Höhe auf \( b \) und erhalten aus dem Satz des Pythagoras:
\( c^{2}=(b-a \cos (\gamma))^{2}+(a \sin (\gamma))^{2}, \)
also
\( \begin{aligned} c^{2} & =b^{2}-2 a b \cos (\gamma)+a^{2}(\cos (\gamma))^{2}+a^{2}(\sin (\gamma))^{2} \\ c^{2} & =b^{2}-2 a b \cos (\gamma)+a^{2}\left((\cos (\gamma))^{2}+(\sin (\gamma))^{2}\right) \\ c^{2} & =b^{2}-2 a b \cos (\gamma)+1 a^{2} \\ c^{2} & =a^{2}+b^{2}-2 a b \cos (\gamma) . \end{aligned} \)
Für den Fall \( \gamma \leq 90^{\circ} \) und \( \alpha>90^{\circ} \) zeichnen wir die Höhe auf \( a \) und erhalten:
\( \begin{aligned} c^{2} & =(a-b \cos (\gamma))^{2}+(b \sin (\gamma))^{2} \\ c^{2} & =a^{2}-2 b a \cos (\gamma)+b^{2}(\cos (\gamma))^{2}+b^{2}(\sin (\gamma))^{2} \\ c^{2} & =a^{2}-2 b a \cos (\gamma)+b^{2}\left((\cos (\gamma))^{2}+(\sin (\gamma))^{2}\right) \\ c^{2} & =a^{2}-2 b a \cos (\gamma)+1 b^{2} \\ c^{2} & =a^{2}+b^{2}-2 a b \cos (\gamma) . \end{aligned} \)
Zuletzt betrachten wir den Fall \( \gamma>90^{\circ} \). Wir zeichnen in ein solches Dreieck die Höhe auf \( b \) und erhalten:
\( \begin{aligned} c^{2} & =\left(b+a \cos \left(180^{\circ}-\gamma\right)\right)^{2}+\left(a \sin \left(180^{\circ}-\gamma\right)\right)^{2} \\ c^{2} & =(b-a \cos (\gamma))^{2}+(a \sin (\gamma))^{2} \\ c^{2} & =b^{2}-2 a b \cos (\gamma)+a^{2}(\cos (\gamma))^{2}+a^{2}(\sin (\gamma))^{2} \\ c^{2} & =b^{2}-2 a b \cos (\gamma)+a^{2}\left((\cos (\gamma))^{2}+(\sin (\gamma))^{2}\right) \\ c^{2} & =b^{2}-2 a b \cos (\gamma)+1 a^{2} \\ c^{2} & =a^{2}+b^{2}-2 a b \cos (\gamma) . \end{aligned} \)
Warum wird hier nach verschiedenen Winkel unterschieden?. 3 Fälle.
Und warum nimmt man immer verschiedene Höhen. Einmal die Höhe auf b. Dann die Höhe auf c.
Falls jemand eine Erklärung hätte wäre das super.
Danke