Kongruenzsatz/Kosinussatz zur Bestimmung von verschiedenen Fällen im Dreieck

Question

Aufgabe:

Es seien a, c > 0 zwei Seitenlängen und α ∈ (0, π/2) ein Winkel.

Benutzen Sie den Kosinussatz, um alle möglichen Dreiecke △(A, B, C) mit ∠A = α, |BC| = a
und |AB| = c zu bestimmen. In welchem Fall gibt es genau ein Dreieck, zwei Dreiecke oder
kein Dreieck mit den geforderten Eigenschaften?

Problem/Ansatz:

Ich verstehe bei der Aufgabe nicht genau, welche Fälle es da geben soll. Ich habe zwei Kanten, die größer 0 sind und einen gegenüberliegenden Winkel mit 0-90°, wenn all diese Dinge gegeben sind, entsteht zwangsläufig ein Dreieck.

Ich glaube ich habe einfach einen Denkfehler bei der Herangehensweise, weil ich auch keine Ahnung habe, wie es überhaupt möglich sein soll, dass daraus zwei Dreiecke entstehen

Answer 1

Es gibt den Kongruenzsatz SsW. Wenn man den der GRÖßEREN Seite gegenüberliegenden Winkel kennt, existiert das Dreieck eindeutig.

Wenn der bekannte Winkel der kleineren Seite gegenüberliegt, kann es zwei, ein oder kein Dreieck geben.

Löse a²=b²+c²-2cb cosα nach b auf und betrachte die Diskriminante der entstehenden quadratischen Gleichung.

wenn all diese Dinge gegeben sind, entsteht zwangsläufig ein Dreieck.

Versuche, ein Dreieck mit c=5,  α=45° und a=1 zu konstruieren. Es geht nicht.

Comments

Auf jeden Fall schonmal vielen Dank, es ist mir definitiv klarer geworden.

Ich hoffe mal, dass meine Diskriminante mit (-c*cos(α))^2 - c^2 + a^2 korrekt ist.

Und als Ergebnis habe ich dann quasi

D<0=/

D=0=1

D>0=2

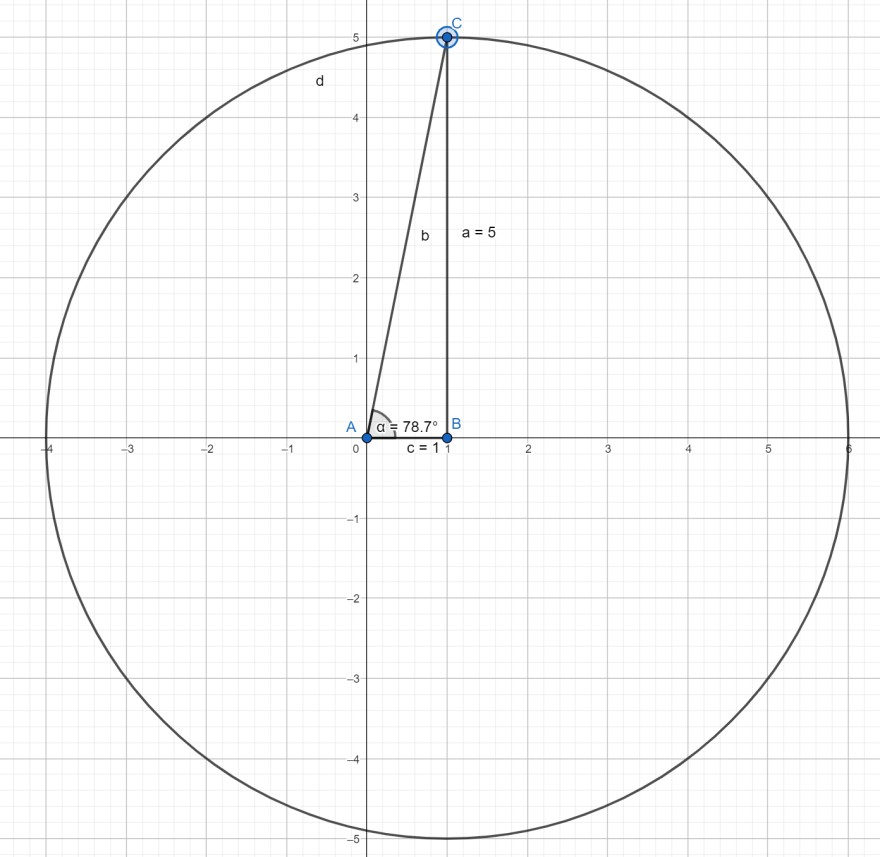
Bloß ergibt dies für mich nicht so richtig Sinn, wenn ich es grafisch zeichne, wenn ich dein Beispiel gerade tausche, also c=1, a=5 und α=45° kommt etwas größer als 0 heraus und es sind zwei Dreiecke, aber wie soll ich das Ganze verstehen. In deinem Beispiel ist der tatsächliche Winkel kleiner als der geforderte, also nicht rekonstruierbar.

In meinem Beispiel ist der Winkel größer, als der, der gesucht wird, wieso bedeutet dies aber nun, dass zwei Dreiecke existieren? Eins mit 45° und noch eins mit kleinerem Winkel oder wie muss ich das verstehen?

---

Die Abbildung zeigt eine gegebene Strecke c mit einem gegebenen anliegenden Winkel α sowie 4 Kreisbögen, deren Radius möglichen vorgegebenen Längen a entsprechen soll. Der innerste Kreisbogen hat einen zu geringen Radius, um den Schenkel des vorgegebenen Winkels zu treffen.

Der nächste Kreisbogen berührt den Schenkel, für diese Länge a gibt es genau eine Lösung.

Der dritte Kreisbogen schneidet den Schenkel zweimal, damit gibt es zwei mögliche Lagen für den Punkt C. Der rote Kreisbogen hat einen Radius a, der größer ist als die Länge c. Damit wird der von A ausgehende Strahl nur einmal geschnitten, und der Punkt C ist wieder eindeutig.

Die blau eingezeichnete Strecke hat übrigens die Länge c*cosα.

Wenn es zwei Schnittpunkte gibt, sind deren Abstände zu A um einen gewissen Betrag kleiner als bzw. um eben diesen Betrag größer als  c*cosα.