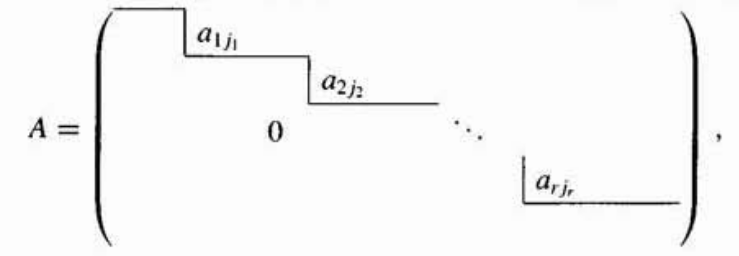
Hallo. Ist \( A = (a_{ij}) \in M(m \times n; K) \) eine Matrix in Zeilenstufenform, so sind die ersten \( r \) Zeilen \( v_1, ..., v_r \) von \( A \) linear unabhängig. Ist nämlich (siehe Bild), so folgt aus \( \lambda_1 v_1 + ... + \lambda_r v_r = 0 \) zunächst \( \lambda_1 a_{1 j_1} = 0 \), also \( \lambda_1 = 0 \) wegen \(a_{1 j_1} \not = 0 \). Meine Frage: Warum ist denn \( \lambda_1 a_{1 j_1} = 0 \)?