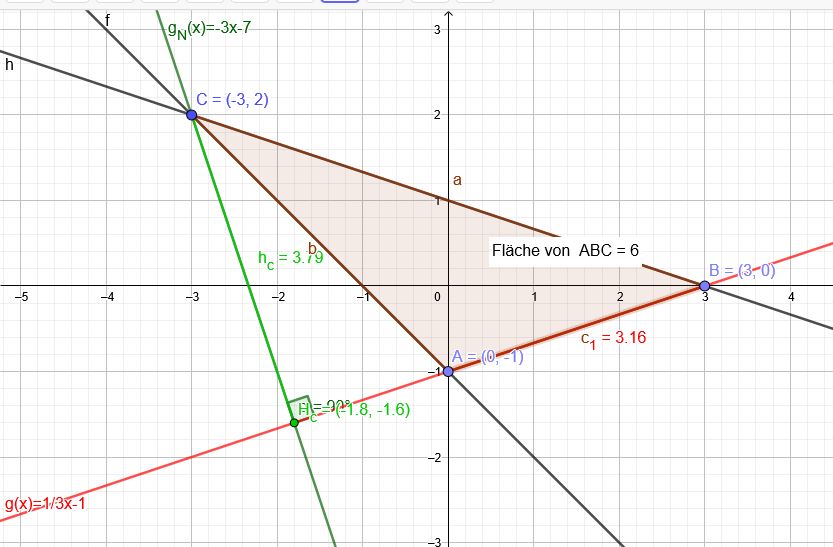
\( A(0 | -1) \) \( B(3 | 0) \) \( C(-3|2) \) Die Punkte A, B und C bilden ein Dreieck. Berechnen Sie den Flächeninhalt dieses Dreiecks.
Der Höhenfußpunkt \(H_c \) liegt auf \(\red{g(x)}=\frac{1}{3}x-1 \) \(m=\frac{1}{3}\) Steigung der Normalen: \(m_N=-3\)
Gleichung der Normalen durch \( C(-3|2) \):
\( \frac{y-2}{x-(-3)}=-3 \) → \( \frac{y-2}{x+3}=-3 \) → \(\green{g_N(x)}=-3x-7 \)
\(\red{g(x)}=\green{g_N(x)} \)
\(\frac{1}{3}x-1=-3x-7 \) →\(x=-1,8 \)→ \(y=-3*(-1,8)-7=-1,6 \)
\(\green{H_c}(-1,8|-1,6)\)
Höhe \(h_c\):
\(h_c=\sqrt{(-3+1,8)^2+(2+1,6)^2}=3,79 \)
Strecke A B=c:\( \sqrt{(3-0)^2+(0+1)^2}=\sqrt{10} \)
\(A= \frac{1}{2}*c*h_c=\frac{1}{2}*\sqrt{10}*3,79≈5,99 \)