Wie würde man das denn zeigen?
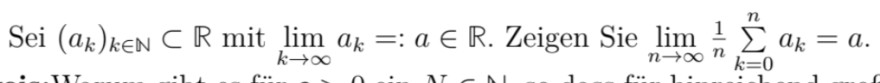
Text erkannt:
Sei \( \left(a_{k}\right)_{k \in \mathbb{N}} \subset \mathbb{R} \) mit \( \lim \limits_{k \rightarrow \infty} a_{k}=: a \in \mathbb{R} \). Zeigen Sie \( \lim \limits_{n \rightarrow \infty} \frac{1}{n} \sum \limits_{k=0}^{n} a_{k}=a \).