Berechnen Sie die Darstellungsmatrix \ell\mathcal{C \leftarrow \mathcal{B}} .

Question

Aufgabe:

Darstellungsmatrix von B nach C

Problem/Ansatz:

Mein Ansatz war es die Darstellungsmatrix als Linearkombination der Basisvektoren von B darzustellen, jedoch hat dies nicht geklappt wie gewollt. Um das ganze als Matrix darzustellen habe ich für die B die Matrix: {{-1,1,1,-1},{1,-2,-3,1},{-1,1,2,-1},{1,-1,-2,0}} und C als Matrix: {{-1,1,1,-1},{1,-2,-3,1},{-1,1,2,-1},{1,-1,-2,0}} erstellt. Dieser Ansatz scheint jedoch falsch zu sein, da ich auf beim Endergebnis nicht auf die gewünschte 3x4 Matrix komme.

Ich wäre dankbar über jede Erklärung und Hilfestellung.

Text erkannt:

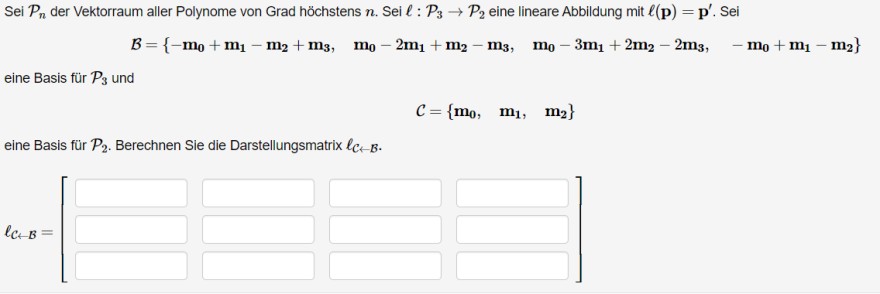
Sei $\mathcal{P}_{n}$ der Vektorraum aller Polynome von Grad höchstens $n$. Sei $\ell: \mathcal{P}_{3} \rightarrow \mathcal{P}_{2}$ eine lineare Abbildung mit $\ell(\mathbf{p})=\mathbf{p}^{\prime}$. Sei
$\mathcal{B}=\left\{-\mathbf{m}_{0}+\mathbf{m}_{1}-\mathbf{m}_{2}+\mathbf{m}_{3}, \quad \mathbf{m}_{0}-2 \mathbf{m}_{1}+\mathbf{m}_{2}-\mathbf{m}_{3}, \quad \mathbf{m}_{0}-3 \mathbf{m}_{1}+2 \mathbf{m}_{2}-2 \mathbf{m}_{3}, \quad-\mathbf{m}_{0}+\mathbf{m}_{1}-\mathbf{m}_{2}\right\}$
eine Basis für $\mathcal{P}_{3}$ und
$\mathcal{C}=\left\{\mathbf{m}_{0}, \quad \mathbf{m}_{\mathbf{1}}, \quad \mathbf{m}_{\mathbf{2}}\right\}$
eine Basis für $\mathcal{P}_{2}$. Berechnen Sie die Darstellungsmatrix $\ell_{\mathcal{C} \leftarrow \mathcal{B}}$.
$\ell_{\mathcal{C} \leftarrow \mathcal{B}}=\left[\begin{array}{l|l|lll} & & & & \\ & & & & \\ & & & & \\ & & & & \\ & & & & \end{array}\right]$

Comments

Mein neuer Ansatz war, dass die Linearkombination für die Vektoren in C: m0=1*(−m0+m1−m2+m3)+0*(m0−2m1+m2−m3)+0*(m 0−3m 1+2m 2−2m3)+0*(−m 0+m 1−m2)

m1=0⋅(−m0+m1−m2+m3)+1⋅(m0−2m1+m2−m3)+0⋅(m0−3m1+2m2−2m3)+0⋅(−m0+m1−m2)

m2=0⋅(−m0+m1−m2+m3)+0⋅(m0−2m1+m2−m3)+1⋅(m0−3m1+2m2−2m3)+0⋅(−m0+m1−m2)

Nach dieser Rechnung würde auf die Lösung {{1,0,0,0},{0,1,0,0},{0,0,1,0}} kommen, ist dieser Ansatz richtig?

---

Dieser Ansatz scheint jedoch auch falsch zu sein. Kann mir bitte jemand die Aufgabe erklären? Ich wäre sehr dankbar über den Input

Answer 1

Aloha :)

Wir definieren uns eine Hilfsbasis $H=\{m_0;m_1;m_2;m_3\}$ mit den Monomen:$$m_0=1\quad;\quad m_1=x\quad;\quad m_2=x^2\quad;\quad m_3=x^3$$Die Abbildung $\ell$, also die Bildung der Ableitung, wirkt auf diese Monome:$$\ell(m_0)=(1)'=0$$$$\ell(m_1)=(x)'=1=m_0$$$$\ell(m_2)=(x^2)'=2x=2m_1$$$$\ell(m_3)=(x^3)'=3x^2=3m_2$$

Die Abbildungsmatrix $L$ für die Abbildung $\ell$ von unserer Hilfsbasis $H$ in die Basis $C$ enthält die Bilder der Basisvektoren als Spalten:$$L_{C\leftarrow H}=\left(\begin{array}{rrrr}0 & 1 & 0 & 0\\0 & 0 & 2 & 0\\0 & 0 & 0 & 3\end{array}\right)$$

Nun sind die Basiselemente der Basis $B$ in Form von Monomen unserer Hilfsbasis $H$ gegeben. Wir kennen daher die Transformationsmatrix von $B$ nach $H$ und brauchen dazu nur die Basiselemente von $B$ als Spalten in eine Matrix zu schreiben:$$T_{H\leftarrow B}=\left(\begin{array}{rrrr}-1 & 1 & 1 & -1\\1 & -2 & -3 & 1\\-1 & 1 & 2 & -1\\1 & -1 & -2 & 0\end{array}\right)$$

Damit erhalten wir die gesuchte Abbildungsmatix:$$L_{C\leftarrow B}=L_{C\leftarrow H}\cdot T_{H\leftarrow B}=\left(\begin{array}{rrrr}1 & -2 & -3 & 1\\-2 & 2 & 4 & \pink{-2}\\3 & -3 & -6 & 0\end{array}\right)$$

Comments

Das Ergebnis ist leider falsch, die Ableitungen habe ich in einem weiterem Versuch auch aufgestellt, jedoch sieht meine \(L_{C\leftarrow H} Matrix etwas anders aus. Liegt da eventuell der Fehler?

---

Ich bin nämlich auf die Matrix \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 3\end{pmatrix} gekommen

---

Habt ihr die Monome in der Vorlesung auch als $m_k=x^k$ definiert?

---

Nicht dass ich wüsste, ist aber gut möglich. So präzise wurde es nie erklärt. Müsste die \(L_{C\leftarrow H} Matrix jedoch nicht 4 Zeilen haben, da vier Monome gegeben sind oder fällt die letzte Zeile aufgrund der Ableitung weg, sodass die Monome wie gewohnt nur in den Spalten stehen?

---

Deine Matrix hat 4 eingehende Dimensionen (Spalten) und 4 ausgehende Dimensionen (Zeilen). Die Ziel-Basis $C$ hat jedoch nur $3$ Dimensionen. Deine Matrix kann also nicht auf $C$ abbilden.

Beispiel: Ableitung von $(x^2+x^3)$ mit meiner Matrix:$$\left(\begin{array}{rrrr}0 & 1 & 0 & 0\\0 & 0 & 2 & 0\\0 & 0 & 0 & 3\end{array}\right)\cdot\begin{pmatrix}0\\0\\1\\1\end{pmatrix}=\begin{pmatrix}0\\2\\3\end{pmatrix}\quad\text{entspricht }(2x+3x^2)$$

---

Jetzt wo ich genauer nachdenke, dann wurden die Monome tatsächlich als $m_k=x^k$ definiert. Das heißt für m0=1, m1=1x, m2=1x^2 usw.

---

Okay verstehe, mein Gedankengang war nicht ganz richtig. Die Matrix $L_{C\leftarrow B}=L_{C\leftarrow H}\cdot T_{H\leftarrow B}=\left(\begin{array}{rrrr}1 & -2 & -3 & 1\\-2 & 2 & 4 & -4\\3 & -3 & -6 & 0\end{array}\right)$ ist leider aber auch nicht korrekt und ich versuche gerade den Fehler herauszufinden, vielleicht fällt er dir schneller auf als mir

---

Ich habe den Fehler gefunden, hatte bei der Matrix-Multiplikation in Excel einen Tippfehler. Habe es oben in pink korrigiert. Es ist nur eine Zahl zu ändern.

---

Ich danke dir vielmals. Der Schritt, dass sich um die einfache Multiplikation von $L_{C\leftarrow H}=\left(\begin{array}{rrrr}0 & 1 & 0 & 0\\0 & 0 & 2 & 0\\0 & 0 & 0 & 3\end{array}\right)$ und  $T_{H\leftarrow B}=\left(\begin{array}{rrrr}-1 & 1 & 1 & -1\\1 & -2 & -3 & 1\\-1 & 1 & 2 & -1\\1 & -1 & -2 & 0\end{array}\right)$ handelt, war mir nicht bewusst. Jetzt weiß ich jedoch für die Zukunft bescheid, vielen Dank nochmals :)

---

Wenn Leerer nicht gut (genug) erklären können, bleiben viele Zusammenhänge im Verborgenen. Deswegen finde ich gut, dass du dich im Netz selber informierst.

---

Leider wird alles zu formell dargestellt, sodass man gar nicht richtig weiß was zu tun ist und dann muss man sich anderweitig informieren. Über Antworten wie deine bin ich dann besonders dankbar, weil es vieles erleichtert.

---

Möglicherweise rührt der Erklärungsbedarf daher, dass Lehrperson einen (technisch geringfügig) anderen Weg zu Bestimmung der darstellenden Matrix vorgestellt hat:

Es gilt etwa für das 1. BasisElement

$$l(-_0+m_1-m_2+m_3)=1 \cdot m_0-2\cdot m_1+3\cdot m_2$$

Daraus liest man die erste Spalte der Darstellungsmatrix ab. Etc.