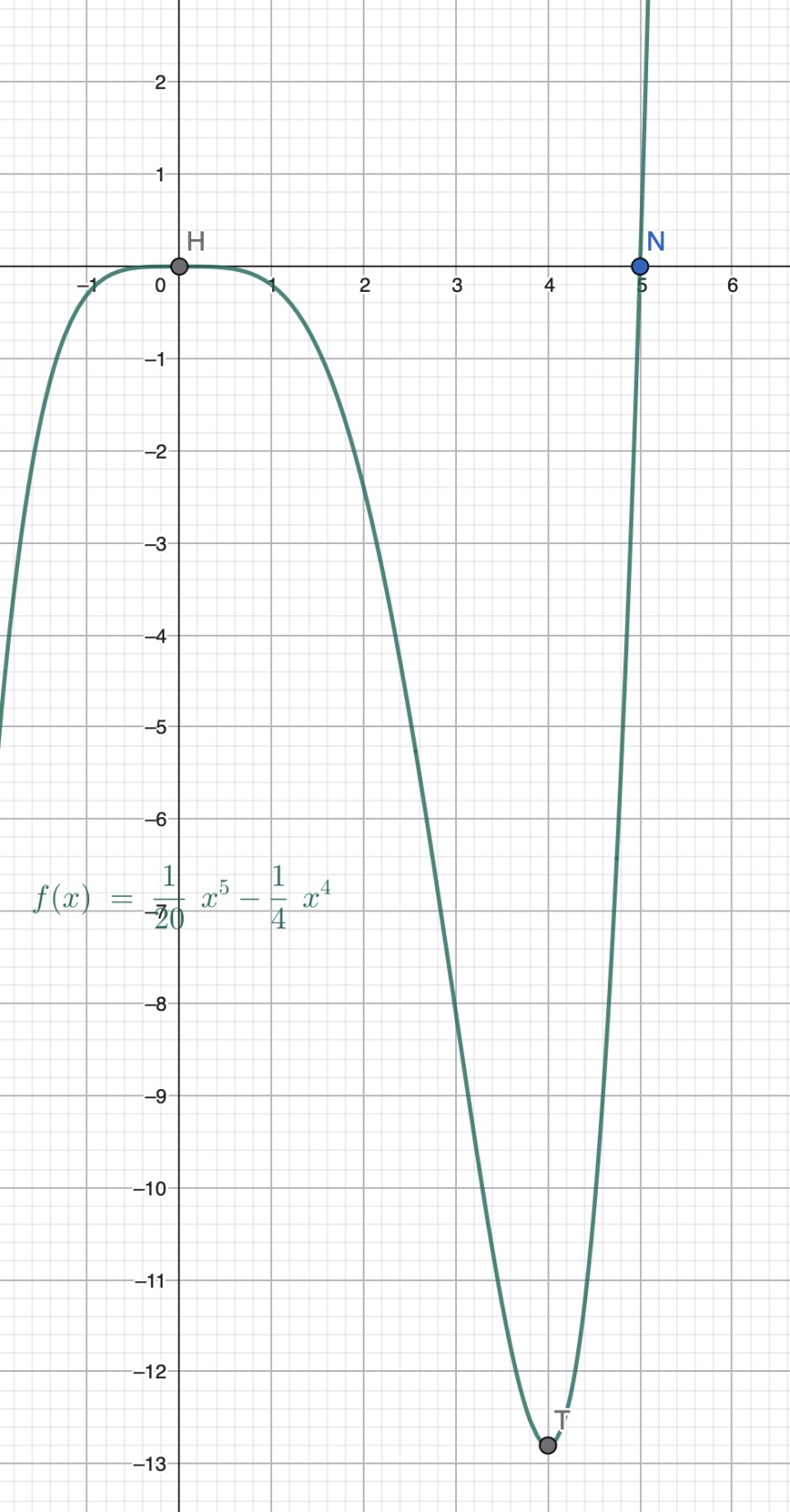
6. Gegeben ist die Funktion \( f(x)=\frac{1}{20} x^{5}-\frac{1}{4} x^{4} \). Sie hat einen Wendepunkt bei \( W(3 \mid-8,1) \)
a) Berechnen Sie die Nullstellen !
\( \frac{1}{20} x^{5}-\frac{1}{4} x^{4}=0 \) Ausklammern von \(x^4\)
\( x^4(\frac{1}{20} x-\frac{1}{4})=0 \) Satz vom Nullprodukt
\( x^4=0 \)
\( x=0 \) ist eine vierfache Nullstelle
\( \frac{1}{20} x-\frac{1}{4}=0 \)
\( x=5 \) ist eine einfache Nullstelle
Berechnen Sie die Extrempunkte !
\( f'(x)=\frac{1}{4} x^{4}- x^{3} \)
\( \frac{1}{4} x^{4}- x^{3} =0\)
\( x^{3}(\frac{1}{4}x -1) =0\)
\( x^{3} =0\)
\( x =0\) \( f(0)=0\)
\( \frac{1}{4}x -1=0\)
\(x=4\) \( f(4)=\frac{1024}{20}-\frac{256}{4} =-12.8 \)
Art der Extremwerte:
\( f''(x)=x^{3}- 3x^{2} \)
\( f''(0)=0\). Der Wert ist weder > noch < 0
\( f'''(x)=3x^{2}- 6x \)
\( f'''(0)=0 \) Der Wert ist weder > noch < 0
\( f''''(x)=6x- 6 \)
\( f''''(0)=- 6 <0\) Maximum
\( f''(4)=256- 48>0\) Minimum
b) Zeichnen Sie den Graphen der Funktion!
c) Ermitteln Sie die Wendetangente der Funktion!
W(3∣−8,1)
\( \frac{y+8,1}{x-3} =f'(3)=\frac{81}{4} - 27=-6,75 \)
\(y=-6,75x+12,15 \)