Ist die f(x)=e^x nach oben beschränkt? e=lim (1+1/n)^n ist ja beschränkt.

Question

Wir machen grad das thema mit limes. Und ich hab da eine sache nicht gut verstanden. E=lim (1+1÷n)^n soll beschränkt sein. Bedeutet das wie oben gefragt, dass die e^x funktion nach oben beschränkt ist. K×(1+p÷n))^n soll auch beschränkt sein. Danke

Answer 1

Es gilt:

$$e=\lim _{ n->\infty  }{ (1+\frac { 1 }{ n } )^{ n } }$$

Dabei ist e die Eulersche Zahl, also e = 2,71828182...

Die genannte Gleichung besagt also, dass der Wert des Ausdrucks

$$\left( 1+\frac { 1 }{ n }  \right) ^{ n }$$

gegen die Zahl

e = 2,71828182...

strebt, wenn man n gegen unendlich gehen lässt. Nach oben beschränkt ist also der Ausdruck

$$\left( 1+\frac { 1 }{ n }  \right) ^{ n }$$

nämlich durch die Zahl e.

 

Die Funktion

f ( x ) = e ^x = 2,71828182... ^x

hingegen ist nach oben unbeschränkt. Sie ist eine Exponentialfunktion, deren Basis die Zahl e ist.

Comments

Ok danke. Sind also streng monoton wachsende funktionen immer nicht nach oben unbeschränkt?

---

Strenge Monotonie sagt nichts über die Beschränktheit aus.

Die Funktion

f ( x ) = e ^x

etwa ist streng monoton wachsend und nach oben nicht beschränkt.

Die Funktion

g ( x ) = ( 1 + 1 / x ) ^x , x > 0

hingegen ist ebenfalls streng monoton wachsend, aber nach oben beschränkt - ihr Wert ist immer kleiner als die Zahl e. 

Answer 2

Ich begebe mich in das Gebiet : Ist es " Haarspalterei " oder lohnt es sich die Frage
absolut exakt anzugehen ?

Zuvor vorab an immai : Du bist in der Lernphase. Deshalb fragst du ja hier.
Mein Kommentar und Antwort sollen helfen deinen  Wissenstand zu erhöhen
und  auch deine Fragen mathematisch richtig zu formulieren.

Frage ( Überschrift ) :

Ist die f ( x ) = e^x nach oben beschränkt ? e lim ( 1 + 1 / n ) ^n ist ja beschränkt.
Meine erster Kommentar  zu
" e lim ( 1 + 1 / n )^n ist ja beschränkt. " ist überhaupt kein mathematischer Ausdruck.
Ist " lim n -> +∞ von ( 1 + 1 / n )^n  beschränkt und gleich e ? "  Ja.
Antwort Teil 1 : der Wertebereich der Funktion f ( x ) = e^x ist  W = ] 0 ..∞ [ .
In Worten : der Wertebereich der Funktion geht von ( ausschließend ) null bis
( ausschließend )  Unendlich. Die Funktion ist nach oben nicht beschränkt.
Die Funktion  ( 1 + 1 / n )^n ist für n > 0 beschränkt auf einen Höchstwert ( e ).
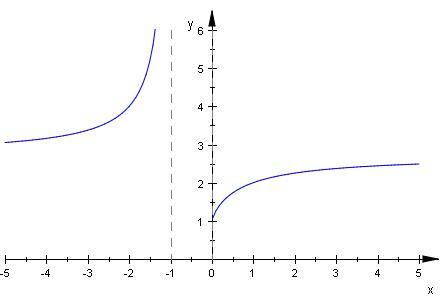
Im gesamten Def-Bereich der Funktion geht die Funktion bei lim n -> (-1)- gegen ∞.

Hier einmal der Graph.

Frage ( Text ) :
Wir machen grad das thema mit limes. Und ich hab da eine sache nicht gut verstanden. E=lim (1+1÷n)ⁿ soll beschränkt sein. Bedeutet das wie oben gefragt, dass die e^x funktion nach oben beschränkt ist.

Antwort : Beide Funktionen sind monoton steigend. e^x geht gegen unendlich ( für x > 0 ).
Die Funktion  ( 1 + 1 / n ) ^n geht für n > 0 gegen einen Grenzwert ( e ).

Erkenntnis : nicht jede monoton steigende Funktion geht gegen ∞, sondern kann auch einem
Grenzwert zustreben. Ein einfaches Beispiel f ( x ) = - (1/x) geht im Bereicih x > 0  bei x -> ∞
gegen Null. Oben rechts auf dieser Seite wäre ein Funktionsplotter zum raschen Zeichnen von
Funktionen.

Frage ( Text ) : K×(1+p÷n))ⁿ soll auch beschränkt sein. Danke
Kann ich nicht interpretieren. Heißt es :
K ( x ) = ( 1 + p / n ))^n ??? Eine rechte Klammer wäre zuviel. Ist p eine Konstante ?
Wo bleibt auf der rechten Seite das x ?

Bei Fehlern oder Fragen wieder melden.
Bin gern weiterhin behilflich.
Nach Durchsicht stelle ich fest das ich mich teilweise
auch nicht mathematisch völlig exakt ausgedrückt habe.

mfg Georg

Comments

Ich danke erstmal und ich werde mich bemühen mich mathematisch korrekter auszudrücken.die formel stand so im skript. P war glaub ich prozentsatz.