Bestimmen Sie die Schnittpunkte mit den Koordinatenachsen.

Question

Schaffe es es nicht auf das Kontrollergebnis dieser Aufgabe zu kommen. Könnte jemand mit dabei helfen?

Gesucht ist eine biquadratische Funktion, die die Ordinatenachse bei y = 5 schneidet
Die Tangente t im Punkt C(-1|0), an den Grafen von f angelegt, hat den Anstieg m = 8,5.
1. Rekonstruieren Sie die Funktionsgleichung. (Kontrollergebnis: y = f(x) = x* - 6,25x2 + 5)
2. Bestimmen Sie die Schnittpunkte mit den Koordinatenachsen.
3. Gesucht wird der Gesamtinhalt der Fläche zwischen dem Grafen von f(x) und der Abszissenachse über dem Intervall I = [-2 / 2].
4. Zeichnen Sie den Graf der Funktion für 2,5 ≤ x ≤ 2,5 und markieren Sie die zu berechnende Fläche.
5. Ermitteln Sie die Gleichung der Tangente t und zeichnen Sie diese ebenfalls in das
Koordinatensystem ein.

Comments

Schaffe es es nicht auf das Kontrollergebnis dieser Aufgabe zu kommen.

Wie sieht denn deine Rechnung aus?

---

Man kommt schon auf die Kontrolllösung. Die zwei gegebenen Bedingungen identifizieren die Funktion f(x) = ax⁴ + bx² + c nicht eindeutig, man kann nachdem man c ermittelt hat über die angegebene Steigung noch einen Parameter frei wählen. In diesem Falle den Koeffizienten von x⁴ einfach als 1, das ergibt -6.25 für b.

Der Aufgabentext sagt ja auch ‚Gesucht ist eine…

---

Die zwei gegebenen Bedingungen

Ich komme auf drei Bedingungen

f(0)=5
f(-1)=0
f'(-1)=8.5

---

Könnte es in der Aufgabe C(-1,-0.25) heißen? Das angegebene C liegt offensichtlich nicht auf der Kontrolllösung (und hatte ich daher mal frech ignoriert).

---

Mit einem Anstieg von m = 7.5 würde es passen. Aber das soll mal der Fragesteller überprüfen, ob es sein Fehler gewesen ist beim Notieren oder die des Lehrers.

---

Aufgabe 4 ist falsch abgeschrieben.

---

Besonders die Exponenten des Kontrollergebnisses f(x) = x* - 6,25x2 + 5 müssen nachbehandelt werden.

---

@Roland: Du fuchtelst doch sonst auch überall in Beiträgen herum und "verbesserst" Rechtschreibung und Grammatik sowie Formalitäten in anderer Leuts Antworten. Wieso machst du nicht jetzt einmal etwas Sinnvolles und verbesserst hier!?

---

Nicht sinnvoll sind hier die Gänsefüßchen.

Answer 1

Schaffe es es nicht auf das Kontrollergebnis dieser Aufgabe zu kommen.

Ich komme auch nicht auf die Lösung. Wie lautet die Vergleichslösung korrekt. Kontrolliere mal die Angaben und die Vergleichslösung.

Ich benutze https://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm

Eigenschaften

f'(0)=0
f'''(0)=0
f(0)=5
f(-1)=0
f'(-1)=8.5

Errechnete Funktion

f(x) = 0,75·x^4 - 5,75·x^2 + 5

Comments

Ich rechne mal mit der gegebenen Funkion weiter.

f(x) = x^4 - 6.25·x^2 + 5

F(x) = 1/5·x^5 - 25/12·x^3 + 5·x

3. Gesucht wird der Gesamtinhalt der Fläche zwischen dem Grafen von f(x) und der Abszissenachse über dem Intervall I = [-2 / 2].

f(x) = x^4 - 6.25·x^2 + 5 = 0 --> x = ± √(50 - 2·√305)/4 ∨ x = ± √(50 + 2·√305)/4

Mit meiner zuerst berechneten Funktion wär's etwas einfacher. Da liegen zwei Nullstellen bei ± 1.

A1 = 2·∫ (0 bis √(50 - 2·√305)/4) f(x) dx = 2·F(√(50 - 2·√305)/4) = √(2318·√305 + 49250)/48 ≈ 6.241

A2 = 2·∫ (√(50 - 2·√305)/4 bis 2) f(x) dx = 2·(F(2) - F(√(50 - 2·√305)/4)) = - √(2318·√305 + 49250)/48 - 8/15 ≈ -6.774

A = |A1| + |A2| ≈ 6.241 + 6.774 = 13.015 FE

Answer 2

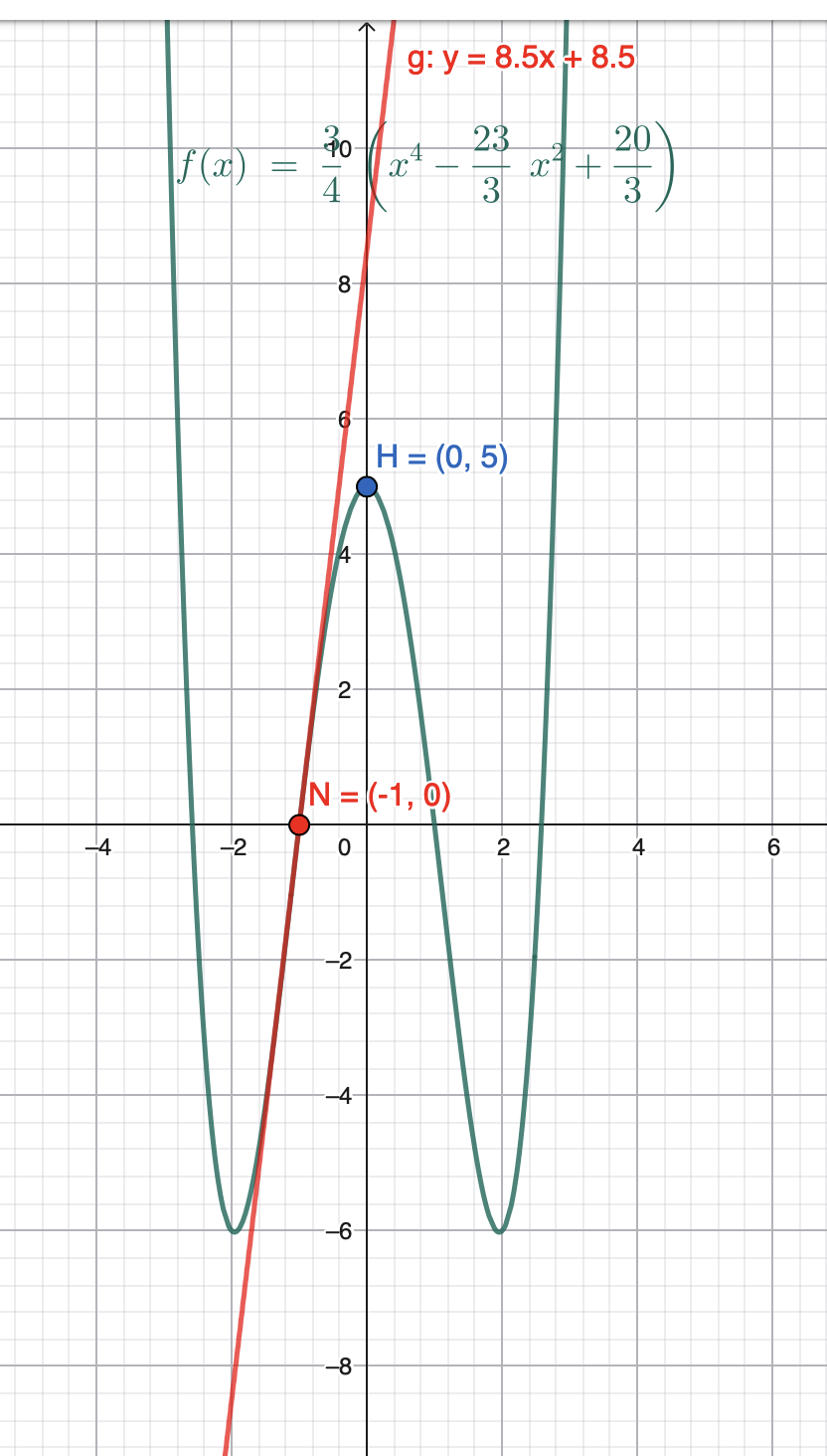
Gesucht ist eine biquadratische Funktion, die die Ordinatenachse bei y = 5 schneidet. Die Tangente t im Punkt C(-1|0), an den Grafen von f angelegt, hat den Anstieg m = 8,5.

Die  biquadratische Funktion bewirkt , dass einfache Nullstellen  bei \(x=-1  \)     und bei   \(x=1  \) existieren.

Linearfaktorenform:

\( f(x)=a(x+1)(x-1)(x+N)(x-N)\\=a(x^2-1)(x^2-N^2)\\=a(x^4-N^2x^2-x^2+N^2) \)

...die die Ordinatenachse bei y = 5 schneidet:

\( f(0)=aN^2=5 \)

\( a=\frac{5}{N^2} \)

\( f(x)=\frac{5}{N^2}(x^4-N^2x^2-x^2+N^2) \)

...Die Tangente t im Punkt C(-1|0), an den Grafen von f angelegt, hat den Anstieg  \( m = 8,5\)

\( f´(x)=\frac{5}{N^2}(4x^3-2N^2x-2x) \)

\( f´(-1)=\frac{5}{N^2}(-4+2N^2+2)=\frac{5}{N^2}(2N^2-2)\)

\(-x^2\frac{5}{N^2}(2N^2-2)=8,5\)

\( N^2=\frac{20}{3}\)

\( a=\frac{5}{\frac{20}{3}} =\frac{3}{4}\)

\( f(x)=\frac{3}{4}(x^4-\frac{20}{3}x^2-x^2+\frac{20}{3})\)

Das Kontollergebnis hat der Fragesteller wahrscheinlich falsch abgeschrieben.