Berechnen Sie den Umfang des Trapezes ABCD.

Question

Text erkannt:

a

Die Eckpunkte des gleichschenkligen Trapezes ABCD liegen auf den Kanten bzw. Eckpunkten einer quadratischen Pyramide.

Es gilt:
\( \begin{aligned} \mathrm{O}_{\mathrm{Pyr}} & =357 \mathrm{~cm}^{2} \\ \mathrm{a} & =10,0 \mathrm{~cm} \\ \overline{\mathrm{AB}} & =\overline{\mathrm{BS}} \end{aligned} \)

Berechnen Sie den Umfang des Trapezes ABCD.

Comments

leider komm ich nicht weiter

---

Das sieht bisher gut und richtig aus.

Beachte das ha bei dir die Seitenhöhe ist.

Berechne den Winkel DSA und die Kantenlänge AS.

Wenn du das hast, könntest du vermutlich auch die Strecke AB im Dreieck ASB und die Strecke BC im Dreieck BSC bestimmen.

Ich komme zum Vergleich auf einen Umfang von etwa 35.49 cm.

---

Ich komme auf 35.52cm

---

Ist wohl eine Realschul-Aufgabe aus 2017, dafür finde ich sie ganz schön happig…

---

Ich hatte mir schon gedacht, dass es für die Realschule war, sonst hätte ich das mit analytischer Geometrie gerechnet.

Deine Abweichung schiebe ich mal auf Rundungsdifferenzen. Geogebra bestätigt mein Ergebnis.

---

ich habe die aufgabe in chat gpt gegeben, und hat mir gesagt, dass AB gleich SB und deshalb der punkt b die seitenkante s halbiert, aber das kann nicht stimmen

---

Das ist korrekt, die KIs rechnen diese Aufgabe alle falsch.

---

Das Problem dabei ist, dass die meisten KI's noch nicht gut trainiert sind mathematische Zeichnungen zu interpretieren. Wenn du es rein textlich formulierst sollte, sofern du das gut machst, eine KI die Aufgabe lösen können.

Ich habe gerade bei https://beta.lmarena.ai/ fünf KI's gegeneinander antreten lassen. Von ChatGPT das Modell o3-mini kam dabei z.B. auf das richtige Ergebnis. Allerdings unter Verwendung der analytischen Geometrie.

Leider hatten claude, deepseek, grok und llama nicht das richtige Ergebnis.

Answer 1

Berechnung
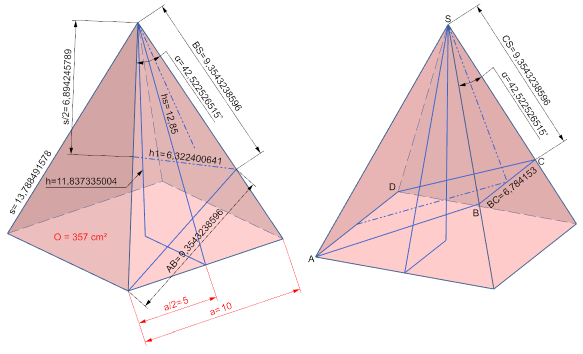
hs = Wurzel( h² + (a/2)² )
hs = Wurzel( 11,837335004^2 + (10/2)^2 )
hs = 12,85 cm
---
h = WURZEL(hs² - (a/2)²)
h = WURZEL(12,85^2 - 5^2)
h = 11,837335004 cm
---
α = arctan((a/2) / hs) * 2
α = arctan(5 / 12,85) * 2
α = 42,522526515°
---
h1 = s/2 * TAN(alpha)
h1 = 6,894245789 * TAN(42,522526515)
h1 = 6,32240064 cm
---
BS = s/2 / COS(alpha)
BS = 6,894245789 / COS(42,522526515)
BS = 9,35432386 cm
---
AB = BS
AB = 9,35432386 cm
CS = 9,35432386 cm
---
BC = WURZEL( CS² + BS² - 2 * CS * BS * cos(α) )
BC = WURZEL( 9,354324² + 9,354324² - 2 * 9,354324 * 9,354324 * cos(42,522527) )
BC = 6,784153 cm
---
Umfang Trapez U
U = a + BC + (BS * 2)
U = AD + BC + (BS * 2)
U = 10 + 6,784153 + (9,354324 * 2)
U = 35,492801 cm

http://texxtorr.bplaced.net/gf/Berechnungen/Pyramide/pyr179-100.png