Wo liegt der Fehler, zwei unterschiedliche Lösungen?

Question

Aufgabe:

Im Folgenden wird die Funktion \( g \) mit \( g(x)=f(x)=-0,025\left(x^{3}-12 x^{2}+36 x-80\right) \) und der Definitionsmenge \( D_{g}=[0 ; 7] \) betrachtet. Der Graph von \( g \) in einem kartesischen Koordinatensystem wird mit \( G_{g} \) bezeichnet.

Der Graph \( G_{g} \), die x-Achse und die beiden Geraden mit den Gleichungen \( x=2 \) und \( x=6 \) schließen ein endliches Flächenstück ein. Berechnen Sie die Maßzahl des Flächeninhalts dieses Flächenstücks.

Hallo, mein Kollege und ich haben zwei unterschiedliche Lösungen, könnt ihr mir eventuell meinen Fehler in der Rechnung aufzeigen?

Comments

Am ende mußt du subtrahieren statt addieren. Übrigens sind die letzten beiden Gleichheitszeichen falsch. Sehr eigenwillige Art, ein bestimmtes Integral auszurechnen. Mach Deine Rechnung unten zu einer Nebenrechnung, dann geht es.

---

Sehr eigenwillige Art, ein bestimmtes Integral auszurechnen.

Könntest du erörtern, was du mit „sehr eigenwillige Art“ meinst, wenn du die Farben meinst, so ist es für mich übersichtlicher.. In der Musterlösungen stehen da auch Gleichheitszeichen vor dem einsetzten der Grenzen

---

Ohne eine Skizze und Begründung ist nicht klar, dass das Integral den Flächeninhalt gibt. Zum Aufschreiben hat user26605 schon alles gesagt, damit hast Du den Fehler schon provoziert. Außerdem multipliziert man nicht den Faktor gleich rein (weiterer Risikofaktor), es sei dann man rechnet gerne und sicher.

---

Ich meine nicht die Farben.

Ich sagte doch, die letzten beiden Gleichheitszeichen sind falsch. Wie rechnet man ein bestimmtes Integral aus?

---

Wie rechnet man ein bestimmtes Integral aus?

Indem man F(6) — F(2) lösen tut (subtrahiert) ja, jetzt sehe ich es auch.

---

Genau, wenn Du F(6) und F(2) einzeln berechnen willst, weil unübersichtliche, längliche Ausdrücke dann ist das ok, aber bitte dann in einer Nebenrechnung und nicht so wie oben.

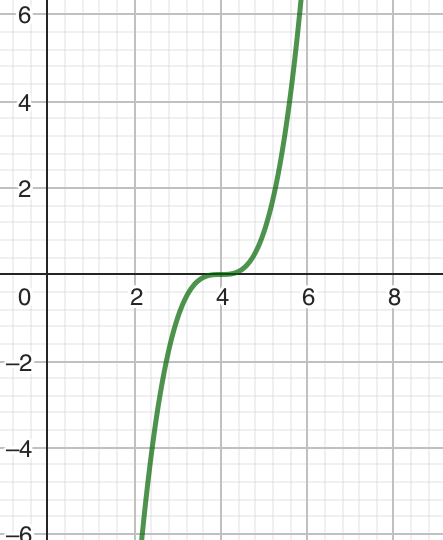
Was fehlt ist noch die Untersuchung, dass f(x) zwischen 2 und 6 nur positive (oder nur negative) Funktionswerte besitzt. Ansonsten müßte man den Integrationsbereich zerlegen, um die Fläche zu bekommen. Dies ist hier nicht der Fall, könnte aber ohne weiteres sein, wie hier:

Answer 1

Letzter Schritt sollte sein

F(6) - F(2) = 93/10 - 29/10 = 32/5 = 6.4

Warum hast du die Ergebnisse addiert?

Skizze