Aufgabe:
Text erkannt:
Aufgabe 9
Einem Investor bieten sich die beiden nachstehend dargestellten Investitionsalternativen.
\begin{tabular}{|l|c|c|c|c|}
\hline & \( \mathrm{t}_{0} \) & \( \mathrm{t}_{1} \) & \( \mathrm{t}_{2} \) & \( \mathrm{t}_{3} \) \\
\hline Investition 1 & -100.000 & 67.000 & 48.000 & - \\
\hline Investition 2 & -120.000 & 60.000 & 45.000 & 36.000 \\
\hline
\end{tabular}
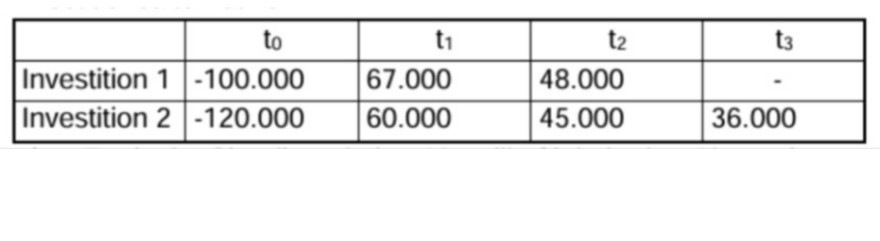
a) Ermitteln Sie die relative Vorteilhaftigkeit der Alternativen unter Verwendung der Kapitalwertmethode. Gehen Sie hierbei von einem Kalkulationszinssatz von 7 \% und anschließend von \( 8 \% \) aus.
b) Zeigen Sie mittels Differenzeninvestitionen auf, dass es sich trotz unterschiedlicher Struktur der Zahlungsreihen um einen zulässigen Vorteilhaftigkeitsvergleich handelt (i \( =8 \) \%).
Problem/Ansatz:
Ich würde gerne Wissen, ob ich beides richtig gerechnet habe und ob meine inhaltlichen Erklärungen stimmen. Leider gibt es bei uns kein Buch, oder Lösungen.
Text erkannt:
a) Ermitteln Sie die relative Vorteilhaftigkeit der Alternativen unter Verwendung der Kapitalwertmethode. Gehen Sie hierbei von einem Kalkulationszinssatz von 7 \% und anschließend von \( 8 \% \) aus.
Schritt 1: Barwert bestimmen
Da die Cashflows nicht als gleichmäßige Annuität gilt, wird wird hier jede Periode diskontiert, um den barwert für jede Periode zu bestimmen.
Investion 1:
\( \begin{array}{l} 67.000 /(1,07)^{1}=62616,82 \\ 48.000 /(1,07)^{2}=41925,05 \\ \text { Barwert }=104541,87 \end{array} \)
Kapitalwert: \( 104541,87-100.000 \rightarrow 4541,87 \)
Investition 2:
\( \begin{array}{l} 60.000 /(1,07)^{1}=56074,76 \\ 45.000 /(1,07)^{2}=39304,74 \\ 36.000 /(1,07)^{3}=29386,72 \\ \text { Barwert }=124766,22 \end{array} \)
Kapitalwert: \( 124766,22-120.000 \rightarrow 24766,22 \)
Investion 1:
\( \begin{array}{l} 67.000 /(1,08)^{1}=62037,03 \\ 48.000 /(1,08)^{2}=41152,26 \\ \text { Barwert=103189,29 } \end{array} \)
Kapitalwert: 103189,29-100.000 \( \rightarrow \) 3189,29
Investition 2:
\( \begin{array}{l} 60.000 /(1,08)^{1}=55555,55 \\ 45.000 /(1,08)^{2}=38580,24 \\ 36.000 /(1,08)^{3}=28577,96 \\ \text { Barwert }=122713,75 \end{array} \)
Kapitalwert: \( 122713,75-120.000 \rightarrow 22713,75 \)
relative Vorteilhaftigkeit eingeschränkte vergleichbarkeit
Text erkannt:
b) Zeigen Sie mittels Differenzeninvestitionen auf, dass es sich trotz unterschiedlicher Struktur der Zahlungsreihen um einen zulässigen Vorteilhaftigkeitsvergleich handelt (i \( =8 \% \) )
Wenn zwei Alternativen unterschiedliche Anfangsinvestitionen haben, vergleicht man sie fair, indem man die teurere durch die günstigere + eine Zusatzinvestition (Differenz) ersetzt. Man prüft dann: Ob sich der höhere Einsatz bei der teureren Alternative lohnt.
Investition 1:
Anschaffung 100.000€
Kapitalwert \( 8 \% \rightarrow 3.189,29 \)
Investition 2:
Anschaffung 120.000€
Kapitalwert 8\% \( \rightarrow \) 22713,75
\( 120.000-100.000 \rightarrow 20.000 € \)
22713,75-3.189,29 \( \rightarrow \) 19.524,46€
Rendite \( \rightarrow \) Kapitalwert / Investition \( \rightarrow \) 19.524,46: \( 20.000 \rightarrow 97,62 € \% \)
Da die Differenzinvestition (20.000 €) einen Kapitalwert von 19.524,46 € erzielt und damit eine Rendite weit über \( 8 \% \), ist der Vergleich zwischen I1 und I2 zulässig.
