Aufgabe:
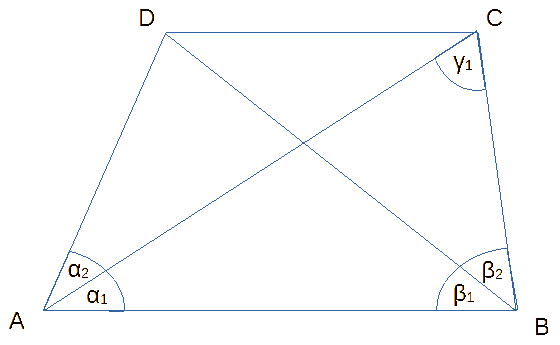
Gegeben sei ein Trapez ABCD, AB parallel zu CD, mit den Winkeln
α1 = BAC,
α2 = CAD,
β1 = ABD.
Wie lassen sich die Winkel
β2 = CBD und
γ1 = ACB
berechnen?
Problem/Ansatz:
Seiten- oder Diagonallängen sind nicht gegeben, die Berechnungen habe ich also auschließlich über die Winkel versucht.
Es ließen sich alle Winkel außer β2 und γ1 berechnen. Für das Problem habe ich auch keine Lösung im Internet gefunden.
Die zeichnerische Konstruktion eines Trapezes mit den gegebenen Winkeln hat funktioniert, entsprechend auch eine Messung des gesuchten Winkels, was allerdings nicht gefragt war.
Text erkannt:
gegebene Winkel:
\( \begin{array}{l} \alpha_{-}=B A C \\ \alpha_{2}=C A D \\ \beta_{-}=A B D \end{array} \)
gesuchter Winkel:
\( \beta_{2}=C B D \)
Text erkannt:
gegebene Winkel:
\( \begin{array}{l} \alpha_{-}=B A C \\ \alpha_{2}=C A D \\ \beta_{-}=A B D \end{array} \)
gesuchter Winkel:
\( \beta_{2}=C B D \)
Text erkannt:
gegebene Winkel:
\( \begin{array}{l} \alpha_{1}=B A C \\ \alpha_{2}=C A D \\ \beta_{1}=A B D \end{array} \)
gesuchter Winkel:
\(
\beta_{2}=C B