Ein neuer geometrischer Satz?

Question

Beweise oder widerlege:

Wenn a und b die Kathetenlängen eines rechtwinkligen Dreiecks EFG sind,

dann ist die Seitenlänge des Quadrats ABCD auch die Höhe des Dreieck EFG.

Comments

Es gibt nicht die Höhe in einem Dreieck.

---

..........................

Answer 1

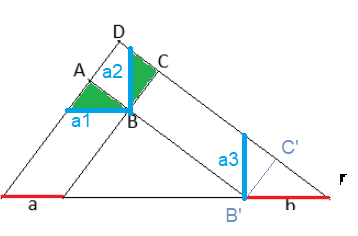
Was parallel aussieht soll auch parallel sein. Gleiches gilt für anscheinend rechte Winkel.

Es sei a1 || a  und a2 || a3.

Die grünen Dreiecke sind (warum auch immer, das überlasse ich der geneigten Leserschaft) kongruent.

Damit gilt a=a1=a2=a3, und die Höhe B'C' im Dreieck mit den Katheten b und a3 hat die gleiche Länge wie die Quadratseite BC.

Roland, vielen Dank für die schöne Aufgabe.

Answer 2

Ich würde gerne mal wissen, wie viel Prozent der Abiturschüler solche Aufgabenstellungen verstehen.

A = 1/2·a·b = 1/2·g·h = 1/2·√(a^2 + b^2)·h

h = a·b/√(a^2 + b^2)

Sei d = |AB| und α der Winkel aus a mit der Verlängerung von AD, dann gilt

a = d/sin(α)

b = d/cos(α)

A = 1/2·a·b = 1/2·g·h

h = a·b / g

h = (d/sin(α))·(d/cos(α)) / √((d/sin(α))^2 + (d/cos(α))^2)

h = |d|

Comments

Ich danke für Hinweise auf suboptimale Formulierung der Aufgabe. Auch der Lösungsvorschlag des Mathecoach ist suboptimal.

Answer 3

Stichwort Höhenquadrat und Höhensatz:

Ich war mal so frei und habe eine passende Illustration herausgesucht.

Quelle: https://mathe.aufgabenfuchs.de/flaeche/dreieck/kathetensatz.shtml

In diesem Fall ist das Quadrat \(ABCD\) also einfach nur das Höhenquadrat des Dreiecks mit den Katheten \(a\) und \(b\), das heißt die Höhe hat die entsprechende Hypotenuse als Grundseite.

Comments

Noch einfacher : Drehe das blaue Dreieck um 90° um den Punkt P.