Seitenlänge 12
Ich schreibs nicht als Lösung hin, weil ich versprochen habe, den Abakus, der diesen Monat überholt werden will, nicht zu überholen.
Drei rechtwinklige Dreiecke und drei Unbekannte, nämlich
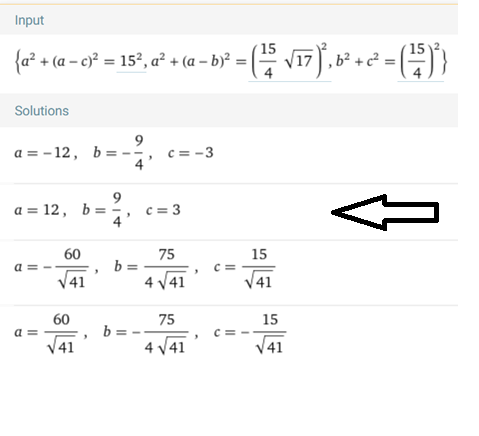
\( a \quad \text{Seitenlänge des Quadrats} \)
\(\displaystyle b = \overline{\vphantom{\big|}DF} \)
\(\displaystyle c = \overline{\vphantom{\big|}DE} \)