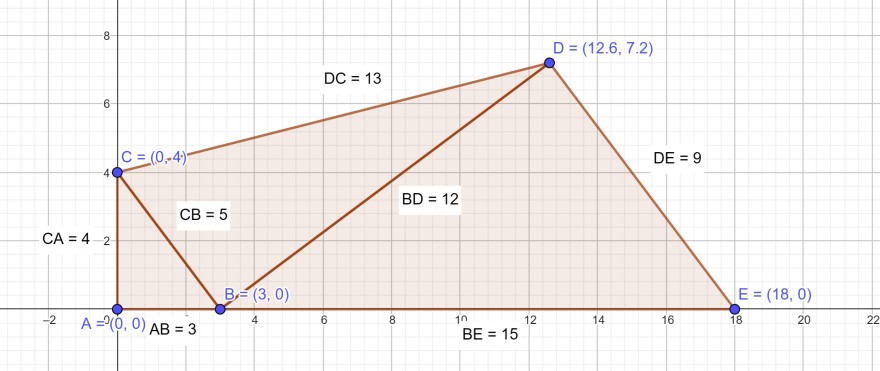
Fläche: 6 + 30 + 54 = 90.
Kleiner dürfte es übrigens nicht gehen.
Beweis:
\((3,4,5)\) und \((5,12,13)\) sind die kleinsten primitiven pyth. Tripel, deren Dreiecksflächen daher auch kleiner sind als alle anderen. Damit die Strecke \(AE\) keine weitere Ecke bildet, muss das Dreieck \(BED\) ähnlich zu \(ABC\) sein und wegen der Kathete 12, kommt dann damit nur ein vielfaches Tripel von \((3,4,5)\), also \((9,12,15)\) in Frage.