wir befinden uns gerade in unserer Abiturvorbereitung ( Hessen) und müssen Präsentationen halten zu gewissen Unterthemen. Wir hatten als Thema jetzt Funktionenscharen , meine andere Partnerin nimmt noch die Kurvendiskussion und die Anwendungungsbezüge unter die Lupe das wäre jetzt mein Teil den ich vortragen würde, ich wollte fragen , ob das ausreicht oder es an gewissen Stellen unnötig ist ( des Weiteren ob auch alles hoffentlich richtig ist ) der Rest folgt im anderen Beitrag

Text erkannt:
b) Für wekhen Wert van a hat der Graph einen Wendepankt an der Stelle \( X=1 \) ?
(1)
\( f_{a}(x)=x^{3}+a x^{2}-\frac{1}{2} a x+2 \)
⇒ not wen dige Bedingung für eine Wende stelle bei \( X=1 \)
(2) \( \quad f_{a}^{\prime \prime}(1)=0 \)
⇒ hinrechende Bedingung for eine Wendestelle bei \( X=1 \)
\( f_{a}^{\prime \prime \prime}(1) \neq 0 \)
Ableitungen
\( \begin{array}{l} f_{a}^{\prime}(x)=3 x^{2}+2 a x-\frac{1}{2} a \\ f_{a}^{\prime \prime}(x)=6 x+2 a \\ (2)=6 \\ f_{a}^{\prime \prime}(x)=6 \end{array} \)
(1)
\( \begin{aligned} f_{a}^{\prime \prime}(1)=6(1)+2 a & =0 \\ 6+2 a & =01-6 \\ 2 a & =-61: 2 \\ a & =-3 \end{aligned} \)
Der Graph van \( f_{-3}(x)=x^{3}-3 x^{2}+1,5 x+2 \) hat einen Wendepnot bei \( x=1 \)
c) Für welche Werte Van a hat der Graph Van \( f a(x) \) Weine Extrempunate?
→ Siehe Seite 3-4.
Weitere Beispiele
\( f a(x)=2 x^{2}-x a+2 a \)
Bestimme, für welche Werte von a der Extrempunkt des Graphen von fa...
a) auf der X-Achse liegt.
b) auf der Y-Achse liegt.
c) auf der Geraden \( y=x \).

Text erkannt:
\( \begin{array}{l} f_{a}(x)=2 x^{2}-x a+2 a \\ \begin{array}{l} f_{a}^{\prime}(x)= 4 x-a \Rightarrow f_{a}^{\prime}(x)=0 \\ 4 x-a=01+a \\ 4 x=a 1: 4 \\ x=\frac{a}{4} \end{array} \\ \begin{array}{l} f_{a}^{\prime}(x)= 4>0 \Rightarrow \text { Tiefpunkt stelle be } x \\ E_{a}\left(\frac{a}{4} \left\lvert\, f_{a}\left(\frac{a}{4}\right)\right.\right)=E_{a}\left(\frac{a}{4} \left\lvert\,-\frac{a^{2}}{8}+2\right.\right) \\ f_{0}\left(\frac{a}{4}\right)= 2\left(\frac{a}{4}\right)^{2}-\left(\frac{a}{4}\right) \cdot a+2 \\ = 2\left(\frac{a^{2}}{16}\right)-\frac{a^{2}}{4}+2 \\ = \frac{a^{2}}{8}-\frac{a^{2}}{4}+2 \\ = \frac{a^{2}}{8}-\frac{2 a^{2}}{8}+2 \\ =-\frac{a^{2}}{8}+2 \\ \text { Ea }\left(\frac{a}{4}\left(-\frac{a^{2}}{8}+2\right)\right. \\ y=0 \end{array} \end{array} \)
Der Extrempunkt liegt auf der X-Achse, wenn die Y-Koordinate gleich Null ist

Text erkannt:
\( \begin{array}{ll} -\frac{a^{2}}{8}+2=01-2 & \\ -\frac{a^{2}}{8}=-21 \cdot(-8) & \text { Ea }\left(\frac{a}{4} \left\lvert\,-\frac{a^{2}}{8}+2\right.\right) \\ a^{2}=161 \pm \sqrt{ } & a=-4 \quad a=4 \\ a_{1,2}= \pm 4 \Rightarrow & \begin{array}{l} \text { Für } a=-4, \text { bzw. } a=4 \text { liegt der Extrempunkt der } \\ \text { Funktion fa(x) auf der X-Achse } \end{array} \end{array} \)
b)
\( \begin{array}{l} \text { Ea }\left(\begin{array}{l} \frac{a}{4} \\ x=0 \end{array}-\frac{a^{2}}{8}+2\right) \begin{array}{l} \text { Der Extrempunkt liegt auf der y-Achse, wenn } \\ \text { die X-Koordinate gleich Null ist } \\ \begin{array}{l} a=0 \\ \frac{a}{4}=01 \cdot 4 \end{array} \Rightarrow E_{0}(0 \mid 2) \\ a=0 \end{array} \end{array} \)
Für \( \mathrm{a}=0 \) liegt der Tiefpunkt auf der y -Achse
c)
\( \begin{array}{l} E a\left(\frac{a}{4} \left\lvert\,-\frac{a^{2}}{8}+2\right.\right) \\ x=y^{2} \\ \frac{a}{4}=-\frac{a^{2}}{8}+2 \left\lvert\, \begin{array}{l} \text { Alles nach links, rechts bleibt } 0 \text { stehen } \\ +\frac{a^{2}}{8} ;-2 \end{array}\right. \\ \frac{a}{4}+\frac{a^{2}}{8}-2=01 \cdot 8 \\ a^{2}+2 a-16=0 \Rightarrow p q \text {-Formel } \end{array} \)

Text erkannt:
\( \begin{aligned} a_{1,2} & =-\frac{2}{2} \pm \sqrt{\left(\frac{2}{2}\right)^{2}-(-16)} \\ & =-1 \pm \sqrt{17} \\ a_{1} & =-1-\sqrt{17}, a_{2}=-1+\sqrt{17} \end{aligned} \)
Für diese Werte von a liegt der Extrempunkt von fa auf der Geraden \( \mathbf{y}=\mathbf{x} \).
Text erkannt:
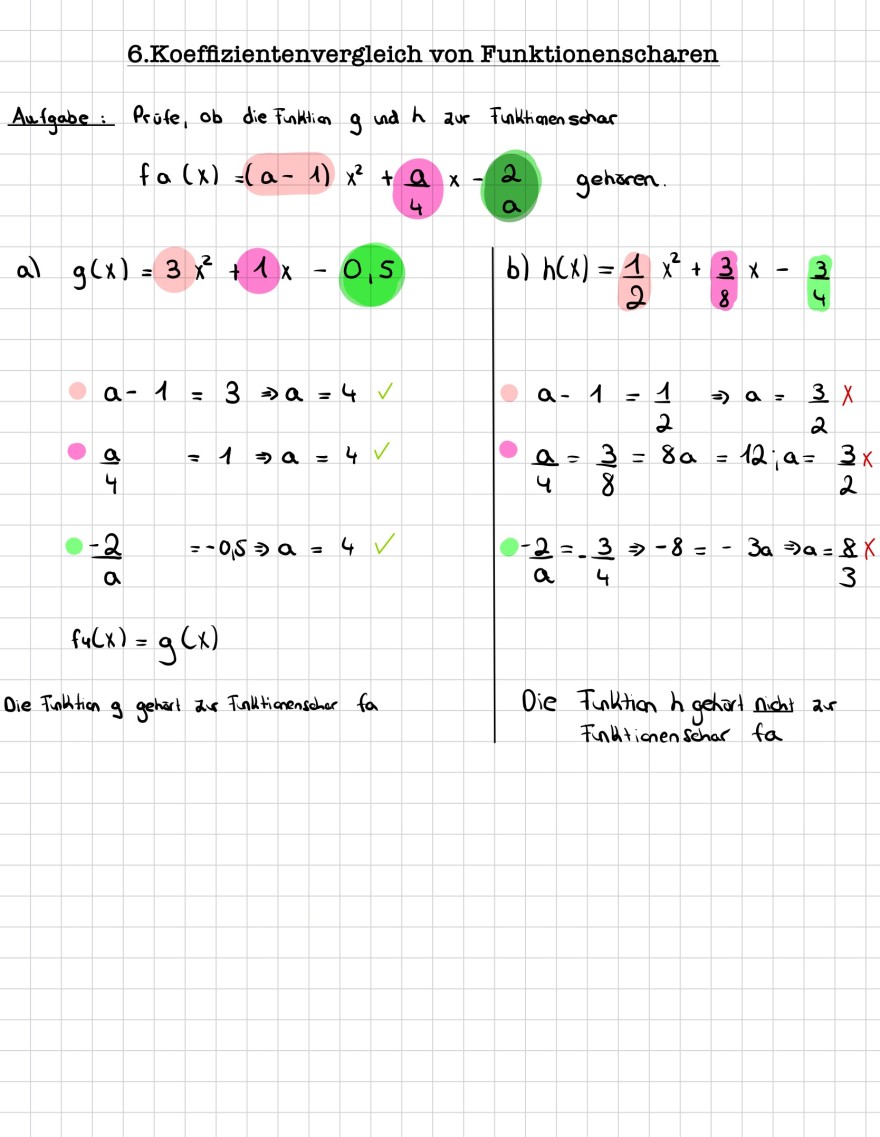
6.Koeffizientenvergleich von Funktionenscharen
Aufgabe: Prüfe, ob die Funktion \( g \) und \( h \) aur Funktionenschar
\( f a(x)=(a-1) x^{2}+\frac{a}{4} x-\frac{2}{a} \text { gehoren. } \)
a) \( g(x)=3 x^{2}+1 x-0,5 \)
\( \begin{array}{l} a-1=3 \Rightarrow a=4 \\ \frac{a}{4}=1 \Rightarrow a=4 \\ \frac{-2}{a} \quad=-0,5 \Rightarrow a=4 \mathrm{~V} \\ f_{4}(x)=g(x) \end{array} \)
Die Funtition a gehart zas Tonltionenschare fa
b) \( h(x)=\frac{1}{2} x^{2}+\frac{3}{8} x-\frac{3}{4} \)
\( \begin{array}{l} a-1=\frac{1}{2} \Rightarrow a=\frac{3}{2} x \\ \frac{a}{4}=\frac{3}{8}=8 a=12 ; a=\frac{3}{2} x \\ -\frac{2}{a}=-\frac{3}{4} \Rightarrow-8=-3 a \Rightarrow a=\frac{8}{3} x \end{array} \)
Die Funktion \( h \) gehart nicht as Funtationenschar fa