Aufgabe Nr. 87/1 von Eigenmann

Question

Aufgabe:

Aufgabe Nr. 87/1  von Eigenmann

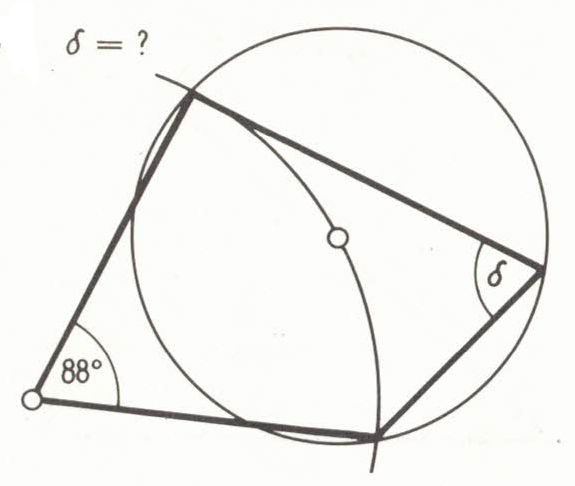
Ohne Taschenrechner; die Figuren sind nicht maßgetreu.

Paul Eigenmann, Aufgabe 1.2.87, ISBN 3-12-722310-2, 1981, S. 14.

Problem/Ansatz:

Muß man annehmen, dass links oben ein rechter Winkel existiert, oder ist das evident?

Comments

Wäre es evident, dann sollte man es auch annehmen. Ich sehe jedoch keinen Grund für einen rechten Winkel. Hingegen sollte man annehmen, dass die Gerade durch die beiden Kreismittelpunkte die Winkelhalbierende des 88°-Winkels ist.

Eigenmann hat auch Lösungen mitgeliefert. Zu dieser Aufgabe schrieb er:

[spoiler]\

\( \displaystyle 68^\circ \)

[/spoiler]

(eingangs zitiertes Werk, S. 57)

---

Muß man annehmen, dass links oben ein rechter Winkel existiert

Nein, aber man muss annehmen, dass der Winkel zwischen 46° und 158° liegt, um die angegebene Lösung zu erhalten.

Answer 1

Muß man annehmen, dass links oben ein rechter Winkel existiert, oder ist das evident?

Nein. Das musst du nicht annehmen. Die sollte auch klar sein, dass sich δ nicht ändert, wenn wir den Winkel auf dem Kreisbogen verschieben.

Es gilt:

α = 88°

δ = 90° - α/4

Also in diesem Fall

δ = 90° - 22° = 68°

Comments

Deine Zeichnung brachte mich darauf, Peripherie-/Zentriwinkel anzuwenden.

Mit dem gleichschenkligen roten Dreieck fand ich den halben Zentriwinkel zu 68°. Der gesuchte Peripheriewinkel ist bekanntlich diesem gleich.

---

Prima. Genau so hab ich mir das gedacht.