Aufgabe:
Gegeben ist der Graph einer ganzrationalen Funktion f vom Grad vier. Es ist Ju die Integralfunktion von f zur unteren Grenze u. Ermitteln Sie, für welche u die Funktion Ju in (u; ∞) keine, genau eine oder mehrere Nullstellen hat.
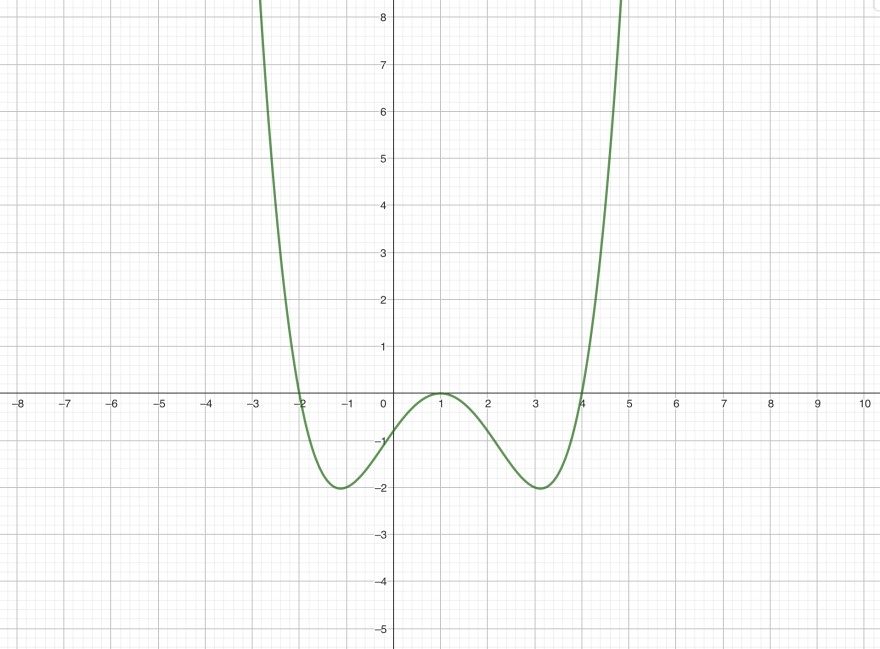
Problem/Ansatz:
Also ich habe mir überlegt, dass für u ≥ 4 Ju keine Nullstellen im Intervall hat und für -2 ≤ u < 4 eine Nullstelle.
Für u < -2 wechselt es bei einem bestimmten Wert a, der kleiner als -2 ist, von ‚keiner Nullstelle‘ wenn u ≤ a, zu ‚zwei Nullstellen‘ wenn a < u < -2.
Aber wie ermittle ich diesen genauen Wert a?