Reelle Funktion 3. Grades - Funktionsterm ermitteln.

Question

Ich komm mal wieder nicht weiter.. geg. ist reelle Funktion h mit h(x)= ax³+bx²+cx  ;  D_h= R. a Element R* = R\{0} ; b,c Element R

Der Graph geht enthält die Punkte P (2|-3) und Q (4|3).

Die Tangente an G_h im Punkt U (0|y_U) verläuft parallel zur Geraden mit der Gleichung 9x + 4y = 0

Berechne sie den Funktionterm von h..

Meine Frage diesbezüglich ist.. wie kann ich methodischc vorgehen.. ich habe mir eine zkizze gemacht, daran konnte ich erkennen, dass der Graph h Punktsymmetrisch zum Koordinatenursprung ist.. also die Funktion die Form : ax³ + cx haben muss.. 

nun hab ich die gleichung nach y aufgelöst um den anstieg der tangente an dem Punkt U herauszufinden..

diesen anstieg habe ich wieder in den allgemeinen Fuktionsterm eingesetzt und nach c aufgelöst..

komme aber nicht auf das ichtige ergebnis...??

hoffe auf schnelle antwort.. danke

Comments

@anemiiie: Hast du das schon durchgelesen?

Soll a auch reell sein oder gar positiv? und ist bei euch R* dasselbe wie R⁺ ?

---

der Definitionsbereich von a ist in der Aufgabenstellung nicht definiert, und R* = R\{0}

ich nehme mal an, dass für a der selbe Definitionsberecht gilt wie für b,c.. wär ja irgendwie nicht logisch.. dann häte ja die funktion keinen anstieg.. ??

das ist eine Prüfungsaufgabe von Bayern 1998.. die unser Lehrer zusammengefasst hat.. leider kann ich ihn heute und morgen nicht mehr erreichen und wir schreiben am Freitag nen Komplextest über alles was wir in den letzten 1,5 Jahren hatten..

---

achso  R^* ist bei uns nicht das selbe wie R⁺ :)

---

Also ist wohl a Element R* = R\{0}

D_h ist bei Polynomen immer R.

Answer 1

Die Tangente an G_h im Punkt U (0|y_U) verläuft parallel zur Geraden mit der Gleichung 9x + 4y = 0

heisst 

du kennst die Steigung von h an der Stelle 0.

Also h'(0)

h(x) = ax^3 + bx^2 + cx

h'(x) = 3ax^2 + 2bx +c

h'(0) = c

Steigung der Geraden: 9x + 4y = 0 umformen.

y = -9/4 x = - 2.25 x

Also c = - 2.25

Du hast nach c gefragt. Ich hab's hier berechnet.

Jetzt musst du nur noch die Koordinaten der beiden gegebenen Punkte einsetzen.

Liefert 2 Gleichungen mit den Unbekannten a und b. Das kannst du dann bestimmt auflösen.

 

Anmerkung. Es ist mir nicht klar, wie du aufgrund der Angaben die Symmetrie begründen willst.

Sicher ist aber, da d=0 ist, dass dein Polynom durch den Punkt N(0/0) geht.

P (2|-3) und Q (4|3).

h(x) = ax^3 + bx^2 -2.25x

h(2) = 8a + 4b - 4.5 = -3

-------> 8a + 4b = 1.5            I. Gleichung

h(4) = 64a + 16 b - 9 = 3

--------> 64a + 16b = 12

            16a + 4b = 3             II. Gleichung

II. Gleichung - I. Gleichung

          8a = 1.5

          a = 3/16

in II. Gleichung einsetzen.

3 + 4b = 3.

b=0 Du hast also wohl recht mit der Symmetrie. 

Mein Resultat:

h(x) = 3/16 x^3 - 2.25x 

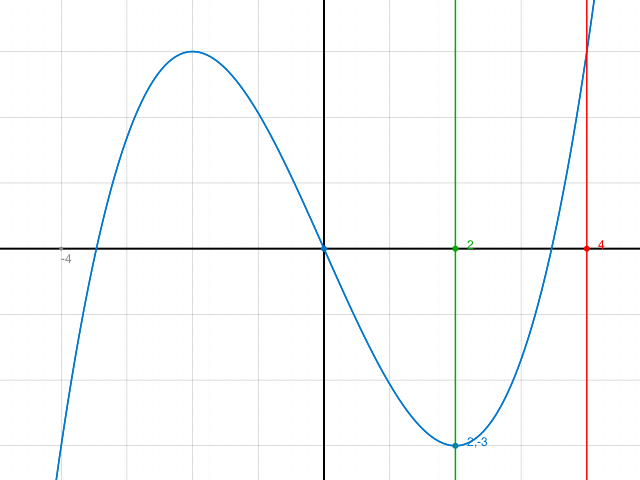
Ausschnitt aus dem Graph:

 

Comments

danke für die schnelle antwort.. ich komm aber leider damit irgendwie nicht weiter..

:(

---

Mein c verstehst du nun? Oder willst du mit deinem c weiterrechnen?

Ich habe übrigens noch fertig gerechnet.