Der Cacher sass bei der Zeitmessung und sah also nur, wie lang die Vorbeifahrt des ersten Zugs dauerte : 6 Sekunden.
Da die beiden Züge mit 81 km/h (= 36 km/h + 45 km/h) aneinander vorbeibrausen, muss man feststellen wie weit man in 6 Sekunden kommt, wenn man mit dieser Geschwindigkeit fährt.
81 km pro Stunde
bedeutet
81000 m pro 3600 Sekunden
gesucht ist die Strecke x,
x m pro 6 Sekunden
Da 3600 : 600 = 6 gibt, muss man auch 81000 durch 600 dividieren
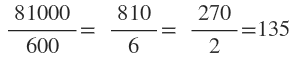
Also misst der erste Zug 135 m.