Quadratische Funktion: Scheitelform, Scheitelpunkt und Nullstellen. f(x)= -¼x^2 + 6x + 9

Question

Hallo :)

Wie rechne ich aus dieser Funktion: f2: f(x)= -¼x² + 6x + 9 Scheitelform, Scheitelpunkt und die Nullstellen aus?

 

Answer 1

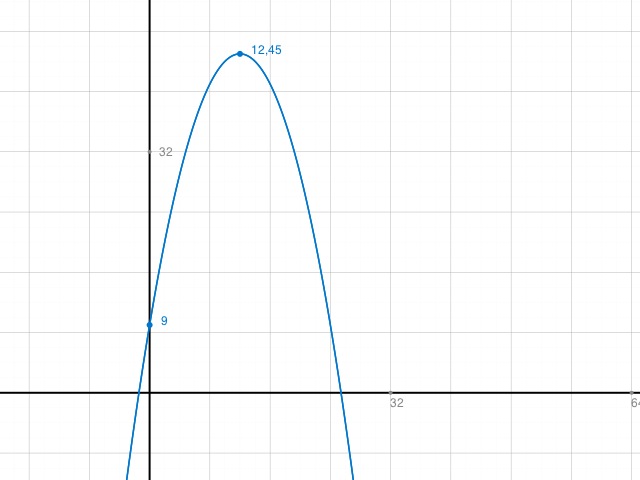
 f(x)= -¼x² + 6x + 9

=  f(x)= -¼ (x² - 24x) +  9

=  -¼ (x^2 - 24x + 12^2 - 12^2) + 9

= -¼ ((x-12)^2 - 144) + 9

= -¼ (x-12)^2 + 36 + 9

= -¼ (x-12)^2 + 45 Scheitelpunktform

S(12 , 45) Scheitelpunkt

Nullstellen:

 -¼ (x-12)^2 + 45 = 0      |*4

-(x-12)^2 + 180 = 0

180 = (x- 12)^2

±√180 = x-12

12 ± √180 = x_1,2

x₁ = 25.416

x₂ = -1.416

Kontrolle: Graph. Schreib Klammern um (12,45) Das sind die Scheitelpunktkoordinaten

 

 

 

Comments

Wie ist den, im ersten und zweitem Schritt, aus der 6x >-24x geworden?

---

 

 f(x)= -¼x² + 6x + 9                    |-¼ ausklammern aus dem ersten Teil.

                                                    |6x / -¼ = 6x*(-4) = -24

Das ist nötig, denn man braucht alles, was mit x zu tun hat um quadr. zu ergänzen.

=  f(x)= -¼ (x² - 24x) +  9

 

---

Oh Gott! Ich hab's ja wirklich verstanden - ein Wunder :D. Vielen, vielen Dank. Du hast mir sehr geholfen!