Aufgabe 1:
Gegeben ist die Funktion f mit der Funktionsgleichung y=f(x)=x²-3x- 7/4 (x ∈ R)
a) Zeichnen Sie den Graph von f mindestens im Intervall -1 ≤ x ≤ 4 in ein Koordinatensystem
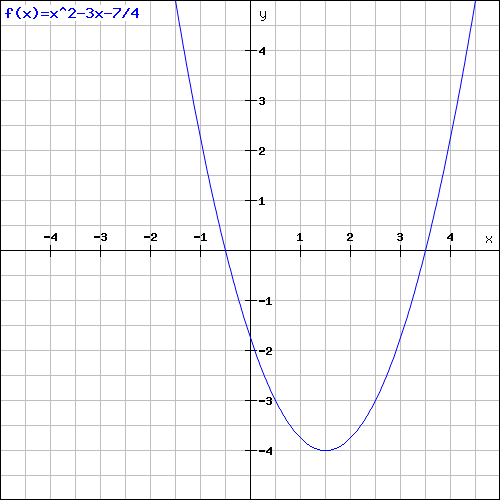
b) Berechnen sie die Nullstelle der Funktion f
f(x) = 0
x^2 - 3x - 7/4 = 0
mit pq-Formel ergibt sich
x1 = 3,5 und x2 = -0,5
c) Zeichnen sie durch den Punkt P(0;1) parallel zur x-Achse eine Gerade.Spiegeln sie den Graph von f an dieser Geraden. Geben sie die Koordinaten des Scheitelpunktes des gespiegelten Graphen an.
Der jetztige Graph hat den Scheitelpunkt zwischen den Nullstellen bei
x = 1/2 * (3,5 + (-0,5)) = 1,5
y = f(1,5) = -4
Der gespiegelte Scheitelpunkt befindet sich also bei S(1,5 | 6)
d) Geben sie die Funktionsgleichung der Spiegelgeraden an
in der Scheitelform lautet sie:
y = -(x - 1,5)^2 + 6
Aufgabe2:
Durch die Gleichung y = x² + 2x - 1,25 (x ∈ R)
a) Berechnen sie die Nullstellen dieser Funktion
x² + 2x - 1,25 = 0
x1 = 0,5
x2 = -2,5
b) Der Graph dieser Funktion ist eine Parable. IHr Scheitelpunkt sei S. Ermittlen sie rechnerisch die Koordinaten von S
x = 1/2 * (0,5 + (-2,5)) = -1
y = (-1)² + 2(-1) - 1,25 = -2,25
S(-1 | -2,25)
c)Zeichnen sie die parable mindestens im Interval -3 ≤ x ≤ 1!
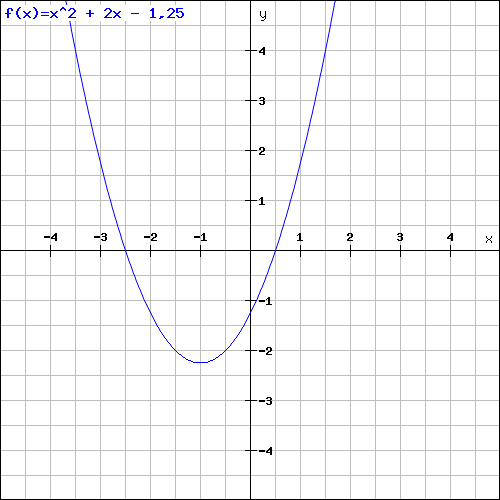
d) Welche Zahl ist in die Gleichung y=x²+2x+q
für q einzusetzen, damit die dadurch gegebene Funktion genau eine Nullstelle hat?
Da wir den Graphen einfach nur um 2,25 nach oben verschieben müssen brauchen wir die Funktionsgleichung
y = x² + 2x - 1,25 + 2,25 = x² + 2x + 1
q muss also +1 sein.