Anm: lb: Abkürzung für binären Logarithmus
0 = y^2 - 1 + lb(x-1)
y = ±√(1-lb(x-1))
2 Äste. Symmetrisch bezüglich x-Achse
1. (1-lb(x-1)) ≥ 0 mach ich hier mal anders (richtiger vgl Link im Kommentar)
1 ≥ lb(x-1) |links und rechts 2^
2^1 ≥ x-1 |+ 1
3 ≥ x.
2. x-1 > 0 stimmt bei deinem Vorschlag
x > 1
Für beide Äste gilt: D = ] 1, 3]
Umkehrfunktion.
0 = y^2 - 1 + lb(x-1) nach x auflösen
1 - y^2 = lb (x-1) |2^links und rechts
2^{1-y^2} = x -1
1 + 2^{1-y^2} = x
x und y vertauschen
y = 1 + 2^{1- x^2} Für D = IR+ Umkehrfunktion von y = √(1-lb(x-1))
Für D = IR- Umkehrfunktion von y = - √(1-lb(x-1))
Bitte noch überprüfen.
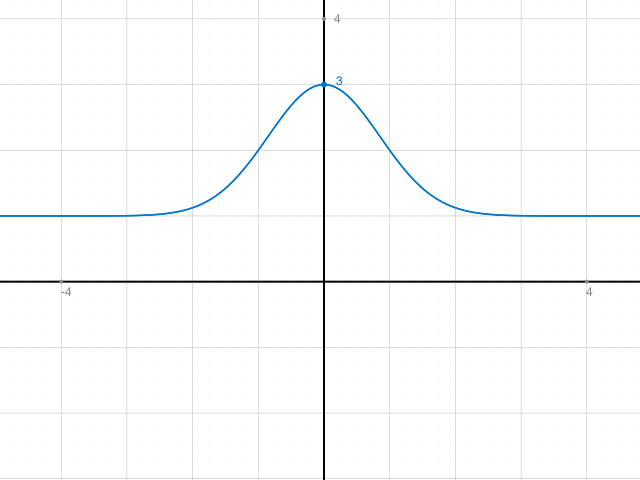
Skizze beider Umkehrfunktionen: