Pralinen werden aufeinander gestapelt. Berechne das Volumen einer Schachtel welche eng an die Figur angelegt wird

Question

Kugelförmige Pralinen werden wie im Bild (unten) aufeinander gestapelt. Die Auflagefläche der äussersten Kugeln bilden ein gleichseitiges Dreieck mit der Seitenlänge 10cm.
 

Berechne das Volumen einer Schachtel, welche eng an die Figur angelegt wird.

 

Ich wäre sehr dankbar wenn mir jemand helfen könnte... 

Comments

Hm. ist jetzt der Radius einer Kugel 10/6 cm ?

Dann würde ich einen Tetraeder um eine Kugel legen, sodass diese Kugel die Innenkugel des Tetraeders ist. Die Seitenlänge dieses Tetraeders müsste dann zu 10 addiert werden und davon das Volumen ausgerechnet werden.

Answer 1

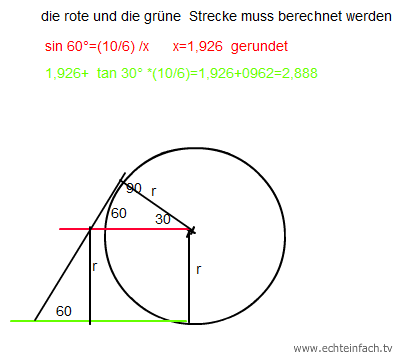
der durchmesser der einzelenen Praline ist :

3*d=10   d=10/3 ⇒ der Radius ist dann r=10/6

ein gleichschenkliges Dreieck , aus denen  sich der Tetraeder der Verpackung zusammen setzt, hat den Winkel von 60°.

dann ist die Grundlinie 10+ 2*2,888=15,777 lang

damit kann man das Volumen  berechnen

V=(a³/12) *√2

V=(15,777³/12) *√2=462,81 cm³

 

 

 

Answer 2

Hier ist das Volumen eines Tetraeders gefragt. Also eine spezielle Dreieckspyramide.

Das Volumen errechnet sich aus:

V = √2/12 * 10^3 = 117,9 cm^3

Wenn du die Formel des Tatraeders nicht im Kopf hast solltest du sie herleiten können. Auf folgender Seite findest du z.b. eine Herleitung:

http://www.mathematische-basteleien.de/tetraeder.htm

Comments

Wie man das Volumen eines Tetraeders berechnet ist mir schon klar... aber diese 10 cm sind ja  die Distanz der Auflage Flächen der untersten Kugeln und nicht einfach die Seitenlängen ;)

---

Wenn ich um eine Kugel mit dem Radius r = 10/6 einen Tetraeder baue dann hat dieser die Kantenlänge:

a = 2·√6·r = 2·√6·10/6 = 10/3·√6

Um diese Länge müsste ich jetzt meinen Tetraeder mit der Kantenlänge 10 erweitern, weil dieser nur durch die äußeren Kugelmittelpunkte geht.

a = 10 + 10/3·√6

Von diesem neuen Tetraeder würde ich das Volumen suchen

V = 1/12·√2·a^3 = 1/12·√2·(10 + 10/3·√6)^3 = 5500·√3/27 + 250·√2 = 706.4 cm^3