Wo liegen die Minima und Maxima dieser Funktionen: f(x)= x/(1+x^2); f(x)=x^4-6x^2-11.

Question

Wo liegen die Minima und Maxima dieser Funktionen?

$$ f ( x ) = \frac { x } { x ^ { 2 } + 1 } $$

$$ f ( x ) = x ^ { 4 } - 6 x ^ { 2 } - 11 $$

Answer 1

f(x)=x^4-6x^2-11

f ' (x) = 4x^3 - 12 x = 4x*(x^2-3) = 0           |faktorisieren

 4x*(x^2-3) = 4x (x-√3)(x+√3) = 0            |3. binomische Forme!

Die Nullstellen der Ableitung, also Extremalstellen:

x1 = 0

x2 =  √3

x3 = -√3

Die zugehörigen Extremalwerte

 

x1 = 0              f(0) = -11                relatives Maximum

x2 =  √3          f(√3)= 9 - 18 - 11 = -20        relatives Minimum

x3 = -√3         f(-√3) = 9 -18 - 11 = -20         relatives Minimum

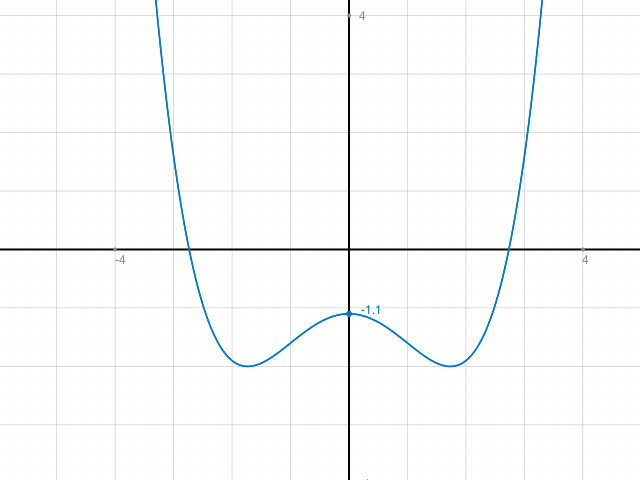
Skizze (Beachte, dass die y-Skala nicht der Realität entspricht! Musste mit Faktor 10 stauchen. Dh. -1.1 entspricht - 11, - 2 entspricht - 20…. Skala in x-Richtung: richtig)

 

Comments

f(x)= x/(1+x^2)                   |Quotientenregel

f ' (x) = ((1+x^2) - x*2x )/ (1+x^2)^2  = 0

genau dann wenn Zähler 0 ist. (Nenner kann hier nie 0 sein)

Zähler: 1 + x^2 - 2x^2 = 1 - x^2 = (1+x)(1-x)  = 0

Extermalstellen:

x1 = -1

x2 = 1

Extremalwerte:

x1 = -1     f(-1) = -1/2       rel. Minimum

x2 = 1       f(1) = 1/2        rel. Maximum