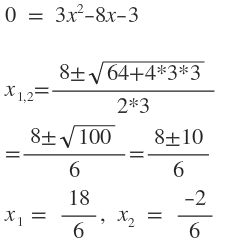Angenommen x ist der Zähler des ersten Bruchs, dann ist x+1 dessen Nenner.
Der erste Bruch ist also x / (x+1)
Um 1 kleiner als der Zähler des ersten Bruchs ist x-1. Als Bruch: (x-1) / 1, da man immer durch 1 dividieren kann, ohne dass sich ein Wert ändert.
Der reziproke Wert (heisst auch Kehrwert) von (x-1)/1 ist 1/(x-1).
Damit erhält man die Gleichung: